- #1
Finding the Area Enclosed by a Polar Curve
Click For Summary
SUMMARY
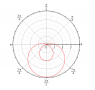
The discussion focuses on calculating the area enclosed by a polar curve defined by the equation \( r = 0.5(1 - 3\sin(\theta)^2) \). The correct limits of integration for this problem are from \( \sin^{-1}(1/3) \) to \( \pi - \sin^{-1}(1/3) \). Participants confirm that these limits are appropriate for determining the area of the polar region, despite concerns about their complexity. The integration should be performed over the specified limits to achieve the correct area result.
PREREQUISITES- Understanding of polar coordinates and polar curves
- Knowledge of integration techniques in calculus
- Familiarity with trigonometric functions and their inverses
- Ability to sketch polar graphs for visual analysis
- Study the derivation of area formulas for polar curves
- Practice integrating polar equations using different limits
- Explore the implications of negative \( r \) values in polar coordinates
- Learn about the graphical representation of polar functions
Students and educators in calculus, mathematicians interested in polar coordinates, and anyone looking to deepen their understanding of integration in polar systems.
- #2
LCKurtz
Science Advisor
Homework Helper
- 9,567
- 775
amninder15 said:
Why did you choose ##-\frac \pi 2## to ##0##? Just guessing? Have you drawn a sketch? Do you know what ##\theta## give negative ##r## values for the inner loop?
- #3
- #4
DryRun
Gold Member
- 837
- 4
Your graph is correct for ##\theta## varies between 0 and 2pi. Now, generally how do you find the area of a polar region?
- #5
LCKurtz
Science Advisor
Homework Helper
- 9,567
- 775
amninder15 said:
Yes. Those are the correct limits. Ugly or not, just plow ahead and you will get one of the answers listed.
Similar threads
- · Replies 3 ·
- · Replies 2 ·
- · Replies 19 ·
- · Replies 13 ·
- · Replies 8 ·
- · Replies 10 ·
- · Replies 2 ·
- · Replies 3 ·