100% transmission through a potential barrier

[Happiness]

A particle of energy $E$ is incident upon a potential barrier of potential $V_0$ and of thickness $a$. Given that $E>V_0$, the transmission coefficient is given by

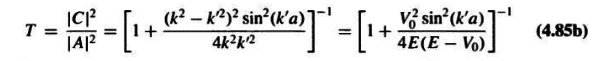
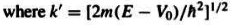
If destructive interference occurs when the path difference between the two reflected waves (at points $x=0$ and $x=a$) is half-integral number of $\lambda'$, then shouldn't constructive interference occurs when the path difference is integral number of $\lambda'$?

 

[jtbell]

The extra path length traveled by the wave that reflects off the back side of the barrier is 2a. That wave travels through the barrier, is reflected off the back side, and travels through the barrier again, in the opposite direction.