OlPhyz
- 6
- 2
Summary:: 12 ton rectangular frame is lowered by a 4 point crane attached to each corner of the frame.
Frame will be lowered onto plastic supports, these supports have guiding ramps of 60 degrees to help the operator lower the frame in the correct spot.
The frame has 4 feet, one on each corner, as the frame is lowered onto the guiding-plastic support what happens to the forces? Especially on the guiding ramp part.
[Mentor Note -- thread moved from the ME forum to the schoolwork forums. This is for a schoolwork project.]
Hello Engineers,
I am coming to you for help with my problem.
Context :
We have a 12 ton frame with 4 aluminium feet. This frame is lifted then lowered onto plastic support spacers.
Lifting is done with 4 cranes attached to the 4 corners of the frame, they lower the frame parallel to the ground. (so the feet are parallel to the ground as they approach the plastic supports, one on each corner where the feet will go)
The frame's lowering speed is not known precisely, but i think we can go with 0.0254 m/s it can probably go slower though.
That will be determined later on, according to the results.
The 4 plastic supports have a 60 degree guiding ramp to help the operator lower the frame on the correct spot on the plastic supports.
We need to know if the plastic will hold lateral forces exerted by the frame as it is touching the guiding ramps.
Knowing what proportion of the 12t is actually being transferred to the plastic spacers would help.
And then a case of looking at the lateral resultant of the applied force.
Problem :
What's the approximate value of the lateral forces transmitted to the plastic supports? (guiding ramp)
Plastic properties :
Yield strength -- 65 MPa
Tensile modulus -- 3000 MPa
Flexural strength -- 115 MPa
Flexural modulus -- 2900 MPa
Friction coefficient -- 0.32
Data Recap :
Frame mass -- 12 tons
Frame lowering speed -- 0.0254 m/s
Point of contact -- Plastic guiding ramp angled at 60 degrees
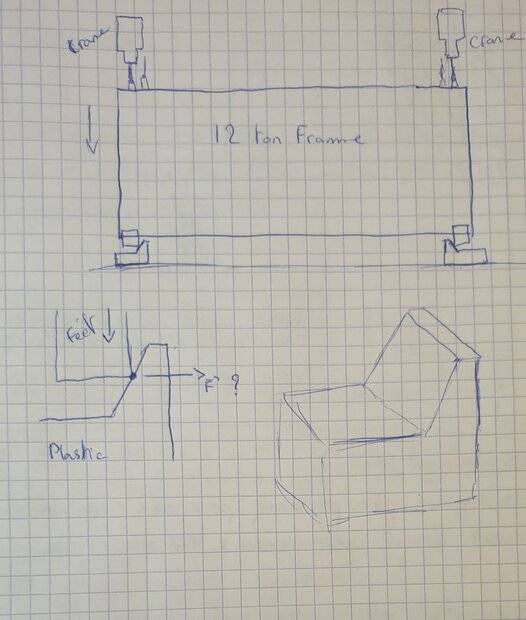
Oh and I just noticed in the image, you might think the two feet are hitting the guiding ramps, this is not the case, only one guiding ramp is used by the operator, the others have enough play so that the feet are not all hitting their respective ramps.
If I missed out on any important details, just tell me.
Thanks for helping out!
Frame will be lowered onto plastic supports, these supports have guiding ramps of 60 degrees to help the operator lower the frame in the correct spot.
The frame has 4 feet, one on each corner, as the frame is lowered onto the guiding-plastic support what happens to the forces? Especially on the guiding ramp part.
[Mentor Note -- thread moved from the ME forum to the schoolwork forums. This is for a schoolwork project.]
Hello Engineers,
I am coming to you for help with my problem.
Context :
We have a 12 ton frame with 4 aluminium feet. This frame is lifted then lowered onto plastic support spacers.
Lifting is done with 4 cranes attached to the 4 corners of the frame, they lower the frame parallel to the ground. (so the feet are parallel to the ground as they approach the plastic supports, one on each corner where the feet will go)
The frame's lowering speed is not known precisely, but i think we can go with 0.0254 m/s it can probably go slower though.
That will be determined later on, according to the results.
The 4 plastic supports have a 60 degree guiding ramp to help the operator lower the frame on the correct spot on the plastic supports.
We need to know if the plastic will hold lateral forces exerted by the frame as it is touching the guiding ramps.
Knowing what proportion of the 12t is actually being transferred to the plastic spacers would help.
And then a case of looking at the lateral resultant of the applied force.
Problem :
What's the approximate value of the lateral forces transmitted to the plastic supports? (guiding ramp)
Plastic properties :
Yield strength -- 65 MPa
Tensile modulus -- 3000 MPa
Flexural strength -- 115 MPa
Flexural modulus -- 2900 MPa
Friction coefficient -- 0.32
Data Recap :
Frame mass -- 12 tons
Frame lowering speed -- 0.0254 m/s
Point of contact -- Plastic guiding ramp angled at 60 degrees
Oh and I just noticed in the image, you might think the two feet are hitting the guiding ramps, this is not the case, only one guiding ramp is used by the operator, the others have enough play so that the feet are not all hitting their respective ramps.
If I missed out on any important details, just tell me.
Thanks for helping out!
Last edited by a moderator: