karush
Gold Member
MHB
- 3,240
- 5
The function f is defined by
$$f(x)=\sqrt{25-x^2},\quad -5\le x \le 5$$
(a) Find $f'(x)$ apply chain rule
$$
\dfrac{d}{dx}(25-x^2)^{1/2}
=\dfrac{1}{2}(25-x^2)^{-1/2}2x
=-\frac{x}{\sqrt{25-x^2}}$$
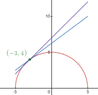
(b) Write an equation for the tangent line to the graph of f at $x=-3$
$$f'(-3)=-\frac{3}{\sqrt{25-(3)^2}}
=-\dfrac{3}{4}=m$$
then f(-3)=4 $y=mx+b$ so $y=-\dfrac{3}{4}(x+3)+4$
(c) Let g be the function defined by $\biggr\{\begin{array}{ll}
f(x) &\textit{for } -5\le x \ge 5\\
x+7 &\textit{for } 3\le x\le 5
\end{array}$
Is g continuous at $x=-3$ (d) Find the value of
$\displaystyle
\int_0^5 x \sqrt{25-x^2}\, dx$
---------------------------------------------------------------
ok i think a and b are okbut (c) x+7 is not a tangent line but looks continuous by the inequalities(d) I assume they tossed in the x for a u substitution method.
View attachment 9331
$$f(x)=\sqrt{25-x^2},\quad -5\le x \le 5$$
(a) Find $f'(x)$ apply chain rule
$$
\dfrac{d}{dx}(25-x^2)^{1/2}
=\dfrac{1}{2}(25-x^2)^{-1/2}2x
=-\frac{x}{\sqrt{25-x^2}}$$
(b) Write an equation for the tangent line to the graph of f at $x=-3$
$$f'(-3)=-\frac{3}{\sqrt{25-(3)^2}}
=-\dfrac{3}{4}=m$$
then f(-3)=4 $y=mx+b$ so $y=-\dfrac{3}{4}(x+3)+4$
(c) Let g be the function defined by $\biggr\{\begin{array}{ll}
f(x) &\textit{for } -5\le x \ge 5\\
x+7 &\textit{for } 3\le x\le 5
\end{array}$
Is g continuous at $x=-3$ (d) Find the value of
$\displaystyle
\int_0^5 x \sqrt{25-x^2}\, dx$
---------------------------------------------------------------
ok i think a and b are okbut (c) x+7 is not a tangent line but looks continuous by the inequalities(d) I assume they tossed in the x for a u substitution method.
View attachment 9331
Attachments
Last edited: