SUMMARY
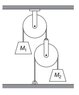
The discussion centers on the constraint equation for a system involving two masses and two pulleys, as presented in "Kleppner and Kolenkow." Participants seek clarification on the division by 2 in the constraint equation for the total length of the strings. It is established that the constraint equation does not accurately represent the total length but rather a fixed quantity related to the system's dynamics. Additionally, the treatment of acceleration (denoted as "a") during the time derivative process is questioned, emphasizing the importance of correctly identifying constants in such equations.
PREREQUISITES
- Understanding of classical mechanics principles, particularly constraints in pulley systems.
- Familiarity with the concepts of time derivatives in physics.
- Knowledge of the specific problem context from "Kleppner and Kolenkow."
- Basic proficiency in mathematical notation used in physics equations.
NEXT STEPS
- Review the derivation of constraint equations in classical mechanics.
- Study the treatment of constants in time derivatives within physics problems.
- Explore examples of pulley systems and their constraints in physics literature.
- Analyze the implications of fixed quantities in dynamic systems.
USEFUL FOR
Students of physics, particularly those studying mechanics, educators teaching classical mechanics concepts, and anyone interested in the mathematical modeling of dynamic systems involving pulleys.