2 methods same answer dynamics

[fahraynk]

In this dynamics MIT open coarseware they are teaching this method where I sum forces on first mass, sum forces on second mass and then sum of torques = change in angular momentum.

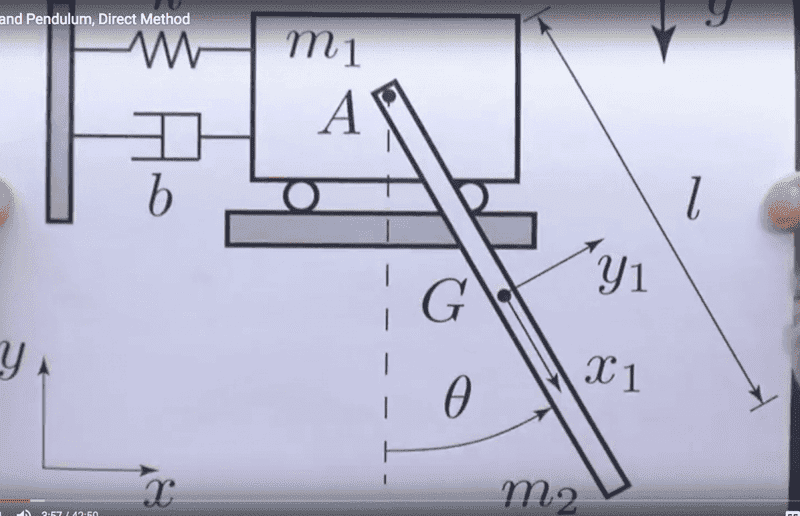
The way I originally learned it was just to look at it and do this :
MX1''=-KX1 - BX1' + M2G/L*(X2-X1) <--(sin(theta)=X2-X1/L for small angles)
MX2''=-M2G/L * (X2-X1)
Why would I want to use the torque/angular momentum equations? Whats the benefit/difference? I am lost and do not see the bridge between what I have been doing and what he is doing.

If interested, simply put this into Youtube search : R7: Cart and Pendulum, Direct Method (don't want to add a link on forum because not sure if there is anti spam or something)

 

[zwierz]

I would say that this problem is rather for the Lagrange equations with generalized force in the right hand side. The generalized force is due to the damper b