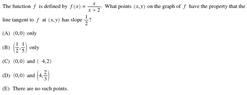224 AP calculus Exam slope at a point (x,y)

[karush]

View attachment 9236
image to avoid typos

Spoiler

$f'(x)=\dfrac{2}{\left(x+2\right)^2}$
so then at slope $\dfrac{1}{2}$
$\dfrac{2}{\left(x+2\right)^2}=\dfrac{1}{2}$
isolate x
$4=(x+2)^2=x^2+4x+4$
then
$0=x(x+4)$
so
$x=0,-4$
thus the slope is $\dfrac{1}{2}$ at $(0,0), and \left(-4,2\right)\quad (C)$

 

[skeeter]

correct

 

[HallsofIvy]

image to avoid typos

Spoiler

$f'(x)=\dfrac{2}{\left(x+2\right)^2}$
so then at slope $\dfrac{1}{2}$
$\dfrac{2}{\left(x+2\right)^2}=\dfrac{1}{2}$isolate x
$4=(x+2)^2=x^2+4x+4$
then
$0=x(x+4)$
so
$x=0,-4$
thus the slope is $\dfrac{1}{2}$ at $(0,0), and \left(-4,2\right)\quad (C)$

This is correct but at $4= (x+ 2)^2$ it is a little simpler to go

immediately​

to $x+ 2= \pm 2$ so that $x+ 2= 2$, $x= 0$ and $x+ 2= -2$, $x= -4$.