2D Relative Velocity, Two Planes

[JKLS]

Homework Statement

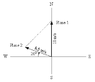
Two airplanes taxi as they approach the terminal. Plane 1 taxies with a speed of 11 m/s due north. Plane 2 taxies with a speed of 8.5 m/s in a direction 20 degrees north of west.

a) What is the magnitude of the velocity of plane 1 relative to plane 2?
b) What is the direction of the velocity of plane 1 relative to plane 2? (in degrees North of East)
c) What is the magnitude of the velocity of plane 2 relative to plane 1?
d) What is the direction of the velocity of plane 2 relative to plane 1? (in degrees South of West)

Homework Equations

The Attempt at a Solution

My main problem here is the setup of the question, as in, where the vectors are placed in reference to one another. The final answers for any of the velocity magnitudes or directions are not provided in the textbook, nor has my professor been willing to meet with me. Also, the question is worded really stupidly.

So, my thinking so far:

The velocities of the two resultant vectors will have the same magnitude, and opposite direction. The vectors aren't merely added, since the addition of these vectors would not result in a vector with a direction in degrees North of East (in its "simplest form"). I attempted to subtract the vector v2 (velocity plane 2) from v1 (velocity plane 1) but the result wasn't accepted by my school's assignment module as correct (~13.5 m/s).

Any ideas?

 

[JKLS]

If anyone can help me with the position of these vectors in relation to one another, and what the question is actually asking, that's all the help I need. The math is super easy, and I can manage questions labeled as much harder than this one fairly quickly. I just need help understanding what this question is asking, and how to set up the vector relationships. Thank you.

 

[JKLS]

I'd still love some help with this one. Just an idea on the setup is necessary... the wording is terrible.

 

[JKLS]

Hello - can someone offer some insight into how to approach this problem? Thank you.

 

[gneill]

Vectors are "translated" to the origin for comparison.

The first step in such problems is to draw a diagram of the vectors involved. Here you go: