2nd Moment of Area, and other questions

[grey]

Hi,

can anyone explain the physical significance of the 2nd Moment of Area? For that matter, it would be nice if you do that for the 1st Moment of Area as well.
I don't want long descriptive answers, because i have read lots of texts already, just want to understand what it is all about.

To be exact, in terms of how much physical the 'physical significance' has to be, I am looking to make a frame that would be subjected to different loads. So before going into CAD and subsequent analysis, I want to do a preliminary static analysis for each member. My aim is mainly to determine which, of the available cross-sections of aluminum, to use for which member of the frame.

So,
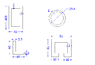
1. I have attached four a pic with dimensions of four available cross sections.
The areas and 2nd moments of areas about the centroidal axis (horizontal one), i list below:
The Rectangular CS: Area = 564 mm², I_XG=727,152 mm⁴
The L-shaped CS: Area = 194 mm², I_XG=28,270 mm⁴
The Circular CS: Area = 75.4 mm², I_XG=5,438 mm⁴
The Square (less some area) CS: Area = 210 mm², I_XG=27,555 mm⁴
What do these values, and the shapes of the cross-sections tell me?

2. Now, in my analysis, I am looking to assume that each member acts as a beam. (the members will eventually be welded). Can i make this assumption without the loss of much accuracy? If yes, why? If no, why?

3. Also, when loads will actually be placed, they physically can not (and might not be intended to) be concentrated loads. For simplicity, can i take them as concentrated loads? I did the bending moment diagram for one section (where a person would sit), and when i took 700N concentrated, max BM was 134Nm for concentrated load, and 116Nm for the load distributed over 20 cm. Clearly, concentrated gives a higher value, and hence an inbuilt safety margin, no?

4. I intend to analyse the members by the trinity we studied in Mechanics of Materials,
f/y = M/I = E/R. Now, M is calculate from lengths of members and loads, I from the cross-sections. E is known, and f depends on y.
So i would get values of previously unknowns R and f from here. But, what would be the limits below which the values of these are safe?
Is it the tensile yield strength of the material (for y)?

 

[grey]

apologies...forgot to upload

all dimensions are 'mm'

 

[minger]

Ah moment of inertias. The first moment of area states that moment that the area creates (an actual moment mind you) is the moment times the distance to the axis. You wind up with
$$\begin{equation} \begin{split} M_x &= A\bar{y} = \int_A y\,dA \\ M_y &= A\bar{x} = \int_A x\,dA \end{split} \end{equation}$$
If you think about this, it can be used to find the centroid of an object. the centroid is an object where all the moments sum to zero.

Now the second moment is similar to the first, but there's an additional distance term multiplied, or:
$$\begin{equation} \begin{split} I_x &= \int y^2\,dA \\ I_y &= \int x^2\,dA \end{split} \end{equation}$$
Second moment of area is an area property that resists bending. It is used in such equations such as:
$$\sigma = \frac{My}{I}$$
The second moment of area, while commonly referred to as moment of inertia by us pesty engineers, is not the moment of inertia.

The moment of inertia, or "Mass Moment of Inertia" is the property which resists angular acceleration, as in:
$$T = I\omega$$
Which is the rotational analogy of
$$F = ma$$

Another good point here, which I've seen incorrectly input into software, and is commonly confused.

Mass Moment of Inertia about an objects axis of rotation is NOT equal to the Polar Moment of Inertia

I see this commonly misused all the time. Polar moment of inertia is the area property which resists torsion. It is analagous to the bending equation in:
$$\tau = \frac{Tr}{J}$$
Where J is the polar moment of inertia. This is not the same as mass moment about the objects axis of rotation.

 

[grey]

Thanks Minger!
Now this is actually what i was looking for (not to mean that the rest of your reply wasn't helpful)

Second moment of area is an area property that resists bending. It is used in such equations such as:
$$\sigma = \frac{My}{I}$$

So, if a cross-section has a greater magnitude of the 2nd moment of area, it would resist bending more?
Also, does a 'greater spread' of material away from the centroidal axis mean it would have a greater magnitude of 2nd moment of area?
and third, once we have calculated the 2nd moment of area of a cross-section, does its shape become useless in further calculations in those like you mentioned:
$$\sigma = \frac{My}{I}$$
?

 

[xxChrisxx]

Yep bigger I value the more resistance to bending.

Take a ruler. 20mm wide 300mm long and 5 mm thick.
The equation for the 2nd moment of area of a rectangle is

I=(bd^3)/12

We know that d gives 3 x the resistance to bending that b does.

d = depth/height
b = breadth/width.

This means that a ruler has two second moment of areas. (This is importatn to bremember as more complicated objects can have more than 1 I value).

using
b = 20mm
d= 5mm

(this is the same as lying it flat o the table)

I = 208.3mm^4

using:
b=5
d=20

(same as standing the ruler up and trying to bend it)

I=3333.3mm^4As you can see the eq shows it much harder to bend a ruler that has the thickness i nthe direction of bending.

 

[grey]

thanks Chris!

ok, one thing...how do i find the centroid (or let's say the centre of mass, assuming uniform mass distribution) of a 3-D figure? And by figure, i don't mean totally solid. Suppose we have a cube with material on 4 of it faces, while the other two are open. AS IN THE DIAGRAM.

Now, if i look at it from the front, i see a square, and i know that its centroid is indeed its geometric centre. But in this case, there is mass (or volume or area if you prefer) in some of its faces that are hidden in the front view. So if we talk about mass, there would be some apparently concentrated at the sides which are material, and their position would effect the position of the centroid.
Anyone?

 

[minger]

The process is the same, except that you need to do it in all three directions. This is the typical case when we take the integral relation, and break it up into a summation.

In laymens terms, it's the summation of total moments, divided by the total area, or:
$$\bar{x} = \frac{\sum^\infty_{n=1} A_n x}{A_{tot}}$$
Where An is the piece's area, x is the distance to the pieces centroid, and Atot is the total area that you're finding the centroid for.

 

[MisterOL]

are there any rules/formulas regarding centroids of certain geometric shapes ?

 

[minger]

Yes. See above. Common sense can be used to quickly calculate the centroid for trivial shapes.
http://en.wikipedia.org/wiki/List_of_centroids

 

[nvn]

Perhaps also try post https://www.physicsforums.com/showpost.php?p=2573083".