grey
- 69
- 0
Hi,
can anyone explain the physical significance of the 2nd Moment of Area? For that matter, it would be nice if you do that for the 1st Moment of Area as well.
I don't want long descriptive answers, because i have read lots of texts already, just want to understand what it is all about.
To be exact, in terms of how much physical the 'physical significance' has to be, I am looking to make a frame that would be subjected to different loads. So before going into CAD and subsequent analysis, I want to do a preliminary static analysis for each member. My aim is mainly to determine which, of the available cross-sections of aluminum, to use for which member of the frame.
So,
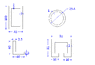
1. I have attached four a pic with dimensions of four available cross sections.
The areas and 2nd moments of areas about the centroidal axis (horizontal one), i list below:
The Rectangular CS: Area = 564 mm2, IXG=727,152 mm4
The L-shaped CS: Area = 194 mm2, IXG=28,270 mm4
The Circular CS: Area = 75.4 mm2, IXG=5,438 mm4
The Square (less some area) CS: Area = 210 mm2, IXG=27,555 mm4
What do these values, and the shapes of the cross-sections tell me?
2. Now, in my analysis, I am looking to assume that each member acts as a beam. (the members will eventually be welded). Can i make this assumption without the loss of much accuracy? If yes, why? If no, why?
3. Also, when loads will actually be placed, they physically can not (and might not be intended to) be concentrated loads. For simplicity, can i take them as concentrated loads? I did the bending moment diagram for one section (where a person would sit), and when i took 700N concentrated, max BM was 134Nm for concentrated load, and 116Nm for the load distributed over 20 cm. Clearly, concentrated gives a higher value, and hence an inbuilt safety margin, no?
4. I intend to analyse the members by the trinity we studied in Mechanics of Materials,
f/y = M/I = E/R. Now, M is calculate from lengths of members and loads, I from the cross-sections. E is known, and f depends on y.
So i would get values of previously unknowns R and f from here. But, what would be the limits below which the values of these are safe?
Is it the tensile yield strength of the material (for y)?
can anyone explain the physical significance of the 2nd Moment of Area? For that matter, it would be nice if you do that for the 1st Moment of Area as well.
I don't want long descriptive answers, because i have read lots of texts already, just want to understand what it is all about.
To be exact, in terms of how much physical the 'physical significance' has to be, I am looking to make a frame that would be subjected to different loads. So before going into CAD and subsequent analysis, I want to do a preliminary static analysis for each member. My aim is mainly to determine which, of the available cross-sections of aluminum, to use for which member of the frame.
So,
1. I have attached four a pic with dimensions of four available cross sections.
The areas and 2nd moments of areas about the centroidal axis (horizontal one), i list below:
The Rectangular CS: Area = 564 mm2, IXG=727,152 mm4
The L-shaped CS: Area = 194 mm2, IXG=28,270 mm4
The Circular CS: Area = 75.4 mm2, IXG=5,438 mm4
The Square (less some area) CS: Area = 210 mm2, IXG=27,555 mm4
What do these values, and the shapes of the cross-sections tell me?
2. Now, in my analysis, I am looking to assume that each member acts as a beam. (the members will eventually be welded). Can i make this assumption without the loss of much accuracy? If yes, why? If no, why?
3. Also, when loads will actually be placed, they physically can not (and might not be intended to) be concentrated loads. For simplicity, can i take them as concentrated loads? I did the bending moment diagram for one section (where a person would sit), and when i took 700N concentrated, max BM was 134Nm for concentrated load, and 116Nm for the load distributed over 20 cm. Clearly, concentrated gives a higher value, and hence an inbuilt safety margin, no?
4. I intend to analyse the members by the trinity we studied in Mechanics of Materials,
f/y = M/I = E/R. Now, M is calculate from lengths of members and loads, I from the cross-sections. E is known, and f depends on y.
So i would get values of previously unknowns R and f from here. But, what would be the limits below which the values of these are safe?
Is it the tensile yield strength of the material (for y)?