A ball hitting a two-ball system (with a spring between them)

[mattlfang]

Homework Statement

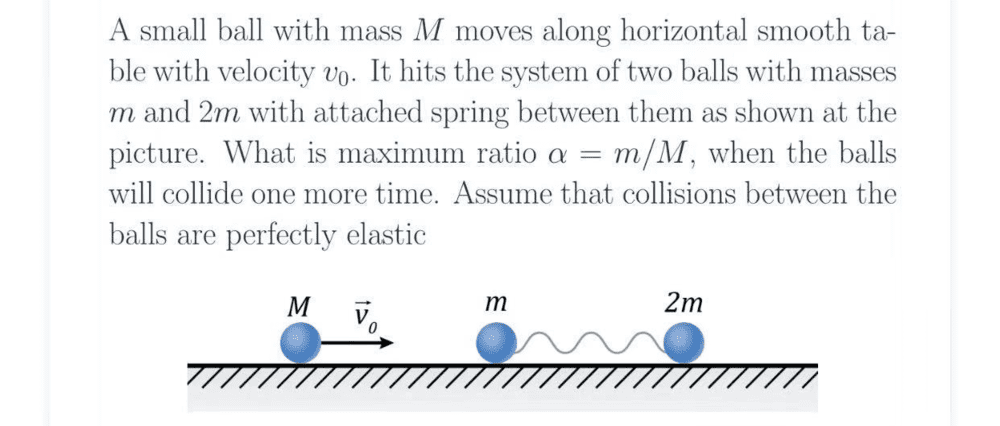
See below chart. A ball with hit a two ball system with a spring in between. What's the maximum ratio of masses so the balls will collide one more time.

Relevant Equations

The law of momentum conservation, The law of energy conservation

I honeslty don't quite know how to start. It seems like the Hooke's coefficent k is independent of the answer to this problem.

I would also appreciate any clue of expressing the condition when "balls will collide again". The fact that all balls can keep moving make this rather difficult.

It seems to me that "balls will collide again" when the speed of M is greater than the speed of the spring attached system (I could be wrong)? But that doesn't help much since the problem only tells me the collision is elastic.

 

[etotheipi]

Here's how I would start. For the initial collision between the $M$ mass and the $m$ mass, assuming this collision is perfectly elastic and instantaneous, the impulse by the spring on the $m$ mass will be zero [since there is, initially, zero extension of the spring]. That means, for this first collision you can ignore the spring, and determine the speeds of the $M$ mass and the $m$ mass just after this initial collision as you would for a simple collision problem.

Then, if the speed of the $m$ mass just after this first collision is $v$ in the lab-frame, the centre of mass of the $m$ & $2m$ mass-spring system moves at $v/3$ in the lab-frame.

In the centre-of-mass frame of the $m$ & $2m$ mass-spring system, the two masses are performing independent oscillatory motion about their initial positions, with the centre of mass stationary. The velocity of the $m$ mass in the centre-of-mass frame of the $m$ & $2m$ mass-spring system right after the initial collision is $2v/3$ to the right.

 

[haruspex]

find the most negative velocity of the m mass in the lab frame?

Isn't it the most negative displacement that's important?

Edit: strike the next part,,, it's more complicated than that. See post #5.

I think your first two paragraphs are enough, stopping at finding the velocity of the common mass centre.

 

[etotheipi]

Isn't it the most negative displacement that's important?

Yeah sorry, you are right, what I said there is incorrect. I just wrote the trajectory in the centre-of-mass frame and transformed the trajectory back to the lab frame, and got an inequality from that.

Hope I didn't confuse you too much, @mattlfang . Let me get rid of the misleading statement.

 

[haruspex]

I think the easiest is the obvious full-frontal approach: to write the equation of motion of mass m and find the closest approach to mass M. None of the usual shortcuts seem to work.

 

[Delta2]

This is a very nice problem, suitable for a physics Olympiad I could say. It seems very counter intuitive that the recollision event doesn't depend on the k of the spring.

Now that I think more carefully, when exactly they recollide must depend on k, but whether they will recollide might be independent of k.

 

[Delta2]

I think the easiest is the obvious full-frontal approach: to write the equation of motion of mass m and find the closest approach to mass M. None of the usual shortcuts seem to work.

What sort of shortcuts did you have in mind? Let me tell my own:
The "naive intuitive" approach:
Find the maximum ratio such that the M ball will continue moving to the right with a speed greater than the speed of the CoM of the system of two masses.
Why this approach won't work?

 

[haruspex]

What sort of shortcuts did you have in mind? Let me tell my own:
The "naive intuitive" approach:
Find the maximum ratio such that the M ball will continue moving to the right with a speed greater than the speed of the CoM of the system of two masses.
Why this approach won't work?

That's the mistake I made at first.
The mass M might strike mass m during the latter's first relatively leftward movement even if the CoM of the two sprung masses moves faster than M. Bear in mind that m starts with the spring at equilibrium; later on it will have a greater length half the time.

 

[Delta2]

That's the mistake I made at first.
The mass M might strike mass m during the latter's first relatively leftward movement even if the CoM of the two sprung masses moves faster than M. Bear in mind that m starts with the spring at equilibrium; later on it will have a greater length half the time.

I see, well what about then to relax the condition, instead of $V_M\geq V_{COM}$ to have $$V_M\geq V_{COM}-\Delta V$$ where $\Delta V$ some velocity quantity that relates somehow to the oscillatory motion of the mass m, but I got no clue how to precisely define it. Maybe you can think more clearly than me.

 

[haruspex]

I see, well what about then to relax the condition, instead of $V_M\geq V_{COM}$ to have $$V_M\geq V_{COM}-\Delta V$$ where $\Delta V$ some velocity quantity that relates somehow to the oscillatory motion of the mass m, but I got no clue how to precisely define it. Maybe you can think more clearly than me.

Timing is important too. Even if the CoM speed of the sprung masses only slightly exceeds that of M, the oscillation won't succeed in making contact if it comes too late.

 

[Delta2]

Timing is important too. Even if the CoM speed of the sprung masses only slightly exceeds that of M, the oscillation won't succeed in making contact if it comes too late.

Hmm, but timing depends surely on k, so you seem to imply that the answer depends on k, but the problem statement implies that the answer doesn't depend on k. There must be some clever shortcut we can't think of at the moment.

 

[wrobel]

Let OX be a fixed horizontal axis. And let $x_1,x_2,x_3$ be the coordinates of the balls.
So that the position of the system is a point $x=(x_1,x_2,x_3)\in \mathrm{R}^3$. This point belongs to a trihedron $A=\{x_1≤x_2≤x_3\}$. The kinetic energy
T=12(Mx˙12+mx˙22+2mx˙32).
defines an inner product in R3.
The miracle is that the point x moves such that it collides and reflects from the boundary of A in accordance with the
"the angle of incidence is equal to the angle of reflection" rule

actually I am tired to correct text everytime when it converts from tex into something what I did not ask to

 

[etotheipi]

I ended up with a condition that, in order for the $m$ and $M$ masses to never collide again, we require that$$(\forall t \in [0, \infty))\, \, \sin( \mathcal{w} t) > \frac{3wt}{2} \left( \frac{M-m}{2M} - \frac{1}{3}\right) = \frac{3 \mathcal{w} t}{2} \left[ \frac{1}{6} - \frac{\alpha}{2} \right]$$where $\mathcal{w} = \sqrt{(3k/2)/m}$ and $\alpha = m/M$. Since the RHS is linear, this just requires that at $t = (3/4)T = (3/4) \cdot (2\pi / w)$, the RHS is less than $-1$, i.e.$$\frac{9 \pi}{4} \left[ \frac{1}{6} - \frac{\alpha}{2} \right]< -1$$which we can then solve for $\alpha$, and then finally negate the statement to find the maximum $\alpha$ at which they do collide again.

 

[haruspex]

I ended up with a condition that, in order for the $m$ and $M$ masses to never collide again, we require that$$(\forall t \in [0, \infty))\, \, \sin( \mathcal{w} t) > \frac{3wt}{2} \left( \frac{M-m}{2M} - \frac{1}{3}\right) = \frac{3 \mathcal{w} t}{2} \left[ \frac{1}{6} - \frac{\alpha}{2} \right]$$where $\mathcal{w} = \sqrt{(3k/2)/m}$ and $\alpha = m/M$. Since the RHS is linear, this just requires that at $t = (3/4)T = (3/4) \cdot (2\pi / w)$, the RHS is less than $-1$, i.e.$$\frac{9 \pi}{4} \left[ \frac{1}{6} - \frac{\alpha}{2} \right]< -1$$which we can then solve for $\alpha$, and then finally negate the statement to find the maximum $\alpha$ at which they do collide again.

To find the necessary and sufficient condition on C s.t. $\sin(\omega t)>Ct$ for all positive t we need to find C s.t. y=Ct is tangent to $y=\sin(\omega t)$ in the range $\pi<\omega t<\frac 32\pi$. I.e. solve $\sin(\omega t)=Ct$ and $\omega\cos(\omega t)=C$.

Squaring and adding to eliminate the trig gives $t^2=\frac 1{C^2}-\frac 1{\omega^2}$, which only has a solution if $|C|<\omega$, but I'm not sure what to deduce from that.

 

[etotheipi]

Ah, you're right, the above condition is not quite strong enough and only approximate. I think to do it exactly, we can look for the first time $\mathscr{t}$ at which the gradients of the two curves are equal, i.e.$$w \cos{w \mathscr{t}} = \frac{3w}{2} \left[ \frac{1}{6} - \frac{\alpha}{2} \right]$$and re-insert this into the previous step

 

[haruspex]

Hmm, but timing depends surely on k, so you seem to imply that the answer depends on k, but the problem statement implies that the answer doesn't depend on k. There must be some clever shortcut we can't think of at the moment.

I think the question setter has underestimated the subtlety and difficulty of the problem.

 

[haruspex]

View attachment 275684

@mattlfang , If this is from a textbook, please identify it.

 

[TSny]

I think you guys have outlined how to solve it. I have no new insights. When I work it through, I get an answer that doesn't depend on $v_0$ or $k$. But the answer does depend on the root of a transcendental equation which arises from @etotheipi's "gradients of the two curves are equal". Here's what I get in case anyone wants to compare answers.

Spoiler

$\large \frac{m}{M} = \frac{1-4\cos\beta}{3}$ where $\beta$ is the smallest positive root of $\beta = \tan \beta$.

$\beta\approx 4.4934$ rad, so $\large \frac{m}{M}$ $\approx 0.623$

 

[haruspex]

I think you guys have outlined how to solve it. I have no new insights. When I work it through, I get an answer that doesn't depend on $v_0$ or $k$. But the answer does depend on the root of a transcendental equation which arises from @etotheipi's "gradients of the two curves are equal". Here's what I get in case anyone wants to compare answers.

Spoiler

$\large \frac{m}{M} = \frac{1-4\cos\beta}{3}$ where $\beta$ is the smallest positive root of $\beta = \tan \beta$.

$\beta\approx 4.4934$ rad, so $\large \frac{m}{M}$ $\approx 0.623$

Now I'm kicking myself because when I first replied to post #11 I wrote that dimensional analysis shows it must be independent of k. Later, it seemed to me that varying k altered the phase of the oscillation in which the recontact would occur, so I mistrusted my analysis.
But I'm still unsure whether the question setter appreciated the subtlety of the question.

 

[TSny]

But I'm still unsure whether the question setter appreciated the subtlety of the question.

I agree.

 

[Delta2]

But I'm still unsure whether the question setter appreciated the subtlety of the question.

We don't know from where this problem is, might be from a physics olympiad and not from a puny textbook...