A child rolls a marble....Plot graphs etc.

[Alexanddros81]

Homework Statement

Serway Physics Section 2.4 Accerleration

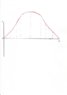
16. A child rolls a marble on a bent track that is 100 cm long as shown in Figure P2.16.
We use x to represent the position of the marble along the track. On the horizontal sections
from x=0 to x=20 cm and from x=40 cm to x=60 cm, the marble rolls with constant speed.
On the sloping sections, the marble's speed changes steadily. At the places where the
slope changes, the marble stays on the track and does not undergo any sudden changes
in speed. The child gives the marble some initial speed at x=0 and t=0 and then watches
it roll to x=90 cm, where it turns around, eventually returning to x = 0 with the same speed with which the child released it. Prepare graphs of x versus t, $v_x$ versus t, and $a_x$ versus t, vertically
alligned with their time axes identical, to show the motion of the marble. You will not be
able to place numbers other than zero on the horizontal axis or on the velocity or
acceleration axes, but show the correct graph shapes.

Homework Equations

The Attempt at a Solution

[/B]

I have drawn the velocity vs time and acceleration vs time. Is this correct?

At velocity vs time graph I am confused with the last slope. It is a positive slope
starting with a negative velocity and ends with less negative velocity. This is the
time that the marble on the way back travels from 40 cm to 20 cm up the slope.
So I am confused if the acceleration should be positive or negative?

 

[jbriggs444]

At velocity vs time graph I am confused with the last slope. It is a positive slope
starting with a negative velocity and ends with less negative velocity. This is the
time that the marble on the way back travels from 40 cm to 20 cm up the slope.
So I am confused if the acceleration should be positive or negative?

You've drawn the velocity versus time curve correctly, showing a negative velocity with a positive slope. You've correctly described the velocity as becoming "less negative" over time.

You could have filled in the relevant equations section with the formula that defines average acceleration: $\frac{v_f-v_i}{\Delta t}$. What does that equation say about the sign of the acceleration in this situation?

 

[Alexanddros81]

We can say that $v_f = -3 m/s$ and $v_i = -6 m/s$
Then $a_{avg} = \frac {-3 - (-6)} {Δt} = \frac {-3 + 6} {Δt} = \frac {+3} {Δt}$
We can see that the average acceleration is positive since numerator and denumerator are both positive.

 

[Alexanddros81]

Here is my answer:

My sketch for x vs t didn't came out that symetrical as it should be.

Is the above correct?

 

[jbriggs444]

It looks good to me.