A Circuit with Nonlinear Element—finding element's current & voltage

[JessicaHelena]

Homework Statement

Lem bought a mystery apparatus at an electrical flea market. One element in the apparatus was unmarked and not obviously identified, but when he measured its behavior in a curve tracer he found that it was a nonlinear resistor with the characteristic shown in Figure 1.

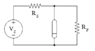
In the circuit that Lem found this the strange element, it was connected to a power supply of 𝑉𝑠=5.0 V with a series resistance of 𝑅𝑠=4700.0Ω and it was shunted with a parallel resistance of 𝑅𝑝=8200.0Ω . (Refer to Figure 2.)

1. What is the current (in Amperes) through the strange object when it is in operation in the circuit?

2. What is the voltage (in Volts) across the strange object when it is in operation in the circuit?

Relevant Equations

KVL, KCL

I don't really understand or see the correct way to approach this.

Letting the current in question be $i_x$ (as shown in Fig. 1), and the unknown (changing) resistance be $R_x$, I can write:
$-V_s + R_s i_s + i_x R_x = 0$, and $R_p i_p = i_x R_x$. Hence we can also write $-V_s + R_s i_s + R_p i_p = 0$.

From KCL I have that $i_s = i_p + i_x$.

Also, $i_s = V_s/(R_s + \frac{1}{\frac{1}{R_x} + \frac{1}{R_p}}).$

Then I have an equation that looks like $V_s + R_pi_x = (R_s + R_p) \cdot i_s$, which doesn't seem to simplify at all...

 

[BvU]

way to approach this

You can ask yourself 'what is the maximum $i_x$ and what is the maximum $V_x$ ?

Note that the suggestive form $R_x$ is only applicable in a certain range of $V_x$ and $i_x$, you want to check what range applies !

 

[gneill]

I might suggest that you first simplify the circuit, combining the known conventional components into a Thevenin equivalent.

Question: Have you covered the concept of load lines in your course? These are very handy when a device has non-linear characteristics. Transistors are a good example of this where you can draw a load line over the characteristic curves to find the operating point.

 

[Babadag]

Up to ix=1 mA Rx=1/0.001=1000 ohm

If ix>1mA[0.001 A] then (vx-1)/(ix-1/1000)=(3-1)/[(2-1)/1000]- ix in A.

Take ix=0.001 A then Rx=1000 ohm and recalculate ix.Then reuse the resulted ix. If you get the same ix eventually that's what you're looking for.