A combination of two potential wells

[Lisa...]

Hi there!

I know how the wavefunctions look like for infinite potential wells and finite potential wells, with the barrier is placed at zero, so I got curious and drew the following well:

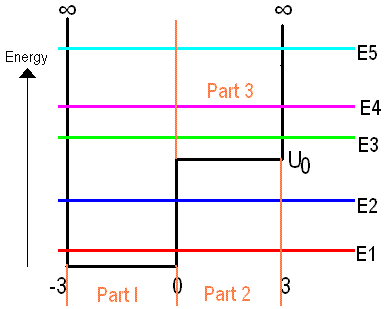
As you can see I split it into three different parts, because the Schrödinger equation has different solutions in each part.

To my opinion the wavefunction needs to equal:

In part 1: A sin(-k3) + B cos(-k3)= B cos(k3) - A sin(k3) (for all Energy levels)
In part 2: D e^(-ax) (for E1 and E2)
In part 3: F sin(k3) + G cos(k3) (for E3 till E5)

So the wavefunctions will look like sines in part 1 and 3 (starting at zero (at x=-3), because the barrier is infinite and ending at zero for the samen reason at x=3). In part 2 the function will be a decreasing exp-function, because of the U0 step in the well, which allows E1 and E2 to leak, though this function needs to be zero at x=3, because there is the infinite barrier.

Ok, so far so good, but how do I know the size of the amplitude for each energy level in each part of the well? And the frequency? (You don't need to explain this mathematically to me, just an explanation of how the frequencies and amplitudes of all energy levels are proportional to each other and why this is so will do ;-)! )

 

[inha]

Well you have three values of x (x=-3,0,3) at which the normal boundary conditions that \psi and it's derivative wrt. x
must be continuous. So by solving the Schrödinger equation for the two different potentials in the well and applying the boundary conditions you'll have enough equations to solve for the unknowns.

edit: the latex is messed up but I'm sure you get what I mean.

 

[Dr Transport]

Almost,
there are 4 areas you must be concerned with, x \leq -3 , -3 < x< 0, 0 < x <\leq 3, x \geq 3 deepending on the energy of the particle there will be different forms of the wave function. outside the well, the wave function will be zero everywhere because the potential is \infty that is the really easy part. Between -3 and 0, the wavefunction will be \sin(k_{1}x) and \cos(k_{1}x) where k_{1} =\sqrt{\frac{2mE}{\hbar^2}}. Here is the hard part, if the energy of the particle is smaller than U_{0} then the wave function is of the form e^{k_{2}x} and e^{-k_{2}x} where k_2 = \sqrt{\frac{2m(U_0 - E)}{\hbar^2}},
If the energy of the particle is larger than U_0 then you will have \sin(k_{2}x) and \cos(k_{2}x) where k_2 = \sqrt{\frac{2m(E - U_0)}{\hbar^2}}. From here all you need to do is match boundary conditions and find the k's.
Take another crack at it and show us what you have done and we will help.

 

[Lisa...]

Ok but how do I need to solve
B cos(k3) - A sin(k3) =0 and A sin(k3) + B cos(k3)=0 ?

Actually the mathematical solution is not very interesting for me.. I'd like to know the amplitudes and the frequencies of the wavefunctions will look like in each part of the well for each energy level, so I don't need to have a numerical value, but I'd like to have an answer like: in E1 the sine has A1, in E2 also, but in E3 it will have an A of 1/2 in part 1 and an A of 2 in part 3.

 

[Lisa...]

Ok, thanks Dr. Transport :) I just missed your post when I replied at first ;)

 

[Lisa...]

I already got stuck here Please help me:

Because there is an infinite barrier at x=-3 in Part 1 the formula is:
Psi(-3)=0 , so B cos(k3) - A sin(k3)=0.
B cos(k3) = A sin (k3)
B sin (k3 - 0.5pi) = A sin (k3)

But here I already got stuck...

same story with Psi(3)=0, so A sin(k3)+ B cos(k3)= 0
B cos(k3) = - A sin (k3)
B sin(k3 - .5pi)= - A sin(k3)

 

[Lisa...]

But is it THAT necessary to solve this problem by doing maths?
You see, I need to make a schematic drawing of the wave function for each energy level. These drawings need to indicate clearly the characteristic features of the wave functions, so it's important for me to know how what kind of shape (sine or exp) the wave function has in which part at which energy level, what happens at the boundaries and most important: what amplitudes and frequencies the wave functions have at which part of the well in which energy level. Again: I don't need to find numerical values, I only need to be able to tell where an amplitude or frequency is for example twice the size of the one of another energy level and why this is so.

 

[Dr Transport]

Outside the well the wave function is zero, so that \psi is zero, this indicates that you have a sine function only. that eliminates the cosines right away. Like I said before, if the energy is less that the potential between 0 and 3, then you have a damped exponential so the wavefunction dies off. if the energy is greater than the potential, the wavefunctin is still sinsoidal. At x = 3, the wavefuntion has to be zero again. At x = \pm 3 gives you the conditions for finding the k's, matching at x = 0 gives you the others. This should be able to give you an idea of how to draw the wave functions quantitively. Remember the k's will be different for x > 0 and x < 0 so your plots w should look different.

 

[Lisa...]

I appreciate your explanation, but is the wave function only a sinusoidal function in x=-3 (without anything with a cos?)? I mean Psi needs to be 0 at -3, and since psi(x)= A sin(kx) + B cos (kx), doesn't this mean that
A sin(-3k)+B cos(-3k)=0 needs to be the wave function?
The same for x=3 (doesn't it mean that A sin(3k) + B cos(-3k)=0 needs to be the wave function?)

 

[Dr Transport]

Since the wave function has to be zero at the boundary, pick the sin. Think about this, take an infinite well between 0 and L. The wave functions are sines and cosines. Apply the boundary condition at 0, this will lead to only keeping the sine.

In your case you have x = -3. OK, think about it, when applying the continuity requirements at x = -3 for the wave function and its derivative, it is much easier to work with pure sines and cosines than mixtures.

Setting the cosine = 0 at x = -3 gives a quanitzation condition on the k which will be
3k = n\pi for all n even giving an energy of E = \frac{\hbar^{2} k^{2}}{2m} = \frac{\hbar^{2} n^{2} \pi^{2}}{18m}.

Much agravation will be had if you try to find these conditoins any other way...

 

[Lisa...]

Ok, now I'm at the stage where I managed to find your given energy quantisation condition (E= (h^2 n^2 pi^2)/18m) for part I of the well and E=((h^2 n^2 pi^2)+18mU0)/18m for part III.

For part 1 I found:

-3k= n pi , so k= (-n pi)/3, therefore the wavefunction is: A sin(((-n pi)/3)x)= -A sin (((n pi)/3)x)

The amplitude is found by taking the integral between -3 and 0 of (-A sin(((-n pi)/3)x)^2 and making it equal 1 (psi^2= the probability and the sum of all probabilities is 1), which gives me A= sqrt(2/3)

For part 3 I found:

3k= n pi , so k= (n pi)/3, therefore the wavefunction is: A sin(((n pi)/3)x)

The amplitude is found by taking the integral between 0 and 3 of (A sin(((-n pi)/3)x)^2 and making it equal 1 which also gives me A= sqrt(2/3).

So what is actually the difference between the frequencies and amplitudes of the wavefunction in part I and III?

 

[Lisa...]

But then again: are you sure it isn't possible to draw the wavefunctions in a qualitative way? I.e. say: the amplitude gets bigger and bigger when the energylevel is higher, the frequency is higher when the energylevel is higher or the amplitude & frequency of the sine in part I is smaller than the one in part III...?

 

[Dr Transport]

It is possible to qualitatively draw the wave functions without solving the math.

In your previous post you said you found the wave function amplitude by integrating, not correct. You have to write down the entire wavefunction andf match the boundary conditions before you can integrate for the amplitudes. The solution of the normalization constants is the last thing you do.

Lets look at this further. For energies greater than U_0, both wavefunctions will be sines. Find the quantization conditions then match the wave functions and their derivatives at x = 0. Work thru the math then from there you can find the normalization constant.

 

[Lisa...]

Allright! Thank you!
This is what I've done till now (all the h's are actually h/2pi 's):

B sin (k1x)= F sin (k2x) for x=0 so
B sin (0) = F sin (0) = 0

(B sin (k1x))' = (F sin (k2x))' for x=0, so
k1B cos (k1 0) = k2F cos (k2x) --> k1B= k2F

k1= sqrt(2mE/h^2) and k2= sqrt((2m(E-U0)/h^2)), therefore:

B sqrt(2mE/h^2) = F sqrt((2m(E-U0)/h^2))

Therefore B= F (sqrt((2m(E-U0)/h^2))) / (sqrt(2mE/h^2)) = F sqrt((E-U0)/E)
And F= B (sqrt(2mE/h^2)) / (sqrt((2m(E-U0)/h^2))) = B sqrt(E/(E-U0))


Therefore B sin(k1x) becomes F sqrt((E-U0)/E) sin (kx).
Because E = (h^2 n^2 pi^2) / 18m, B sin(k1x) becomes
F sqrt (((h^2 n^2 pi^2) / 18m)-U0)/(h^2 n^2 pi^2) / 18m)) =
F sqrt ((h^2 n^2 pi^2)-18mU0)/ (h^2 n^2 pi^2).

So now we know that the sine in region I has a factor sqrt ((h^2 n^2 pi^2)-18mU0)/ (h^2 n^2 pi^2) extra in it's amplitude compared to the sine in region III (F sin (k2x)).

Therefore I can conclude that the amplitudes in region I will be smaller than in region III and they will grow in size when the energy levels are going up.

****** Is this correct?
*********** What about the frequencies of the two sines? Are they the same for the sine in region I and region III? In my previous post I found k to be k= (n pi)/3 for both sines...

 

[Lisa...]

Nvm on calculating... I asked my teacher today and he told me that I need to draw the relative differences in amplitudes and frequencies for all energy levels WITHOUT calculating anything! Could someone please tell me if all amplitudes in region I (for every energy level) are the same? (so we'll see the same amplitude in region I for E2 and E3, though the amplitude of the last top in region III on E3 is bigger than E2)? And why there are always two tops of the sine in region I and the rest of them in region III?(so always two tops in region I, and for E3 1 top in III, for E4 2 tops in III etc) And why are the amplitudes of the sine in region III bigger than in region I?