A Direct approach to Kepler's Orbits

[danielakkerma]

Hello everyone!
After having being asked to help prepare a simulation(using computer programming), for the general(numerical) solution to Kepler's orbits(strictly speaking, for any central force, and for simplification, no other is acting here), I ran into a bit of a rut trying to resolve some outstanding issues applying to this problem.
Naturally I am aware of the general solution as it pertains to Polar coordinates, but I've decided to try out solving directly for planar motion on the x,y field.
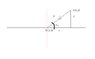
Here are my equations(and also, please see the diagram attached)
Assuming a central force:
<br /> \large<br /> \vec{F}=-\vec{\nabla}U = \frac{k}{r^2} <br />, Where k is a constant should determine the course of the motion(i.e its being parabolic, hyperbolic, circular, that sort of thing).
In the cartesian coordinate system(the one I use):
<br /> \large<br /> r^2=x^2+y^2 <br />
Which leads to:
<br /> m\ddot{\vec{r}} = \frac{k}{r^2}\hat{r}<br />
Bifurcating the force to the axes:
<br /> m\ddot{x} = \frac{k}{r^2}\cos{\phi}, <br /> m\ddot{y} = \frac{k}{r^2}\sin{\phi},<br /> \phi = \arctan{\frac{y}{x}}<br />
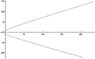
Naturally these systems have only a numerical solution, and, in doing so, I've received the following output which doesn't make any sense to me, the graph, irrespective of the initial conditions(and of k), leads to conflicting outcomes, which you can evaluate for yourself.
I'll let the images speak for themselves,
I can't thank you enough in advance for your attention to this rather tedious question,
Beholden,
Daniel
P.S
The so-called "ImageA" is plot of (x, y).

 

[Philip Wood]

Thank you for such a graceful request. The problem may be that you haven't specified initial velocity components. [You don't say that you have.] What you have set up is two second order differential equations. For each equation the first integration will throw up an arbitrary constant which you can specify in terms of the initial velocity components. Doing it numerically won't avoid this requirement. [If your automated integration has made its own choice of arbitrary constants, these might be equivalent to putting the initial velocity components at zero, meaning that the planet will plunge into the Sun along a radius.]

You probably know that the slick way to solve the problem is to start out with equations based on conservation of energy and of angular momentum. This way you've already done, as it were, the first integration, and you put in your initial velocity right at the beginning.]

 

[danielakkerma]

Hi there Phillip, thanks for a very prompt reply.
You pinpointed a very acute problem, as related to the specifications of Initial conditions.
Obviously, I've had to supply them, But in doing so for x'[t] and y'[t], I've found it difficult to obtain any reasonable difference by manipulating them. Furthermore, for different Ks I pretty much got the same results, which is very suspicious.
Integrating the equations below is rather tricky, because both depend on Phi, which is itself a function of y/x;
As for the conservation of Energy & Angular momentum, though it's plain they would have(and in fact, that's what I have been using heretofore) yielded the answer very commodiously, I still wanted to tackle the problem head on, Getting a direct elucidation for X and Y, as will be more suitable for my program code.
Regarding the initial conditions, is there any advice you can grant on what I should set, just so we could observe a shift in the plot? I've honestly tried nearly every possible combination.
In the image I had provided, I had set up, x(0) == R(some value) y(0) = 0, x'(0)=v1 y'(0) = v2, and let it solve, without much success though, appearantly :(..
Very thankful as always,
Daniel

 

[vanhees71]

I don't understand the plot. What's on the axis?

Despite the already pointed out problem with the incomplete initial conditions, I would not use the angle, \phi. The formula you use to calculate it, is for sure wrong. Either use the function atan2 (as it's named in FORTRAN or its equivalent in other programming language) or its explicit form

\mathrm{atan2}(y,x)=\sign y \arccos \frac{x}{\sqrt{x^2+y^2}},

which is numerically expensive and good for nothing or just use Cartesian coordinates to obtain the trajectory. If you want the angle, you can use the above equation afterwards anyway.

To control the numerical stability, it's also good to plot energy and angular momentum vs. time to check whether these quantities are conserved within your numerics (for the exact solution, of course they are conserved exactly!).

 

[danielakkerma]

Hi there, thanks for a swift response here..
The plot shows an x, y scatter plot, of the two functions solved, individually, for x[t] and y[t].
As for the angle considerations, though I find you're of course right, I still don't see how I would partition the force, which is radial, on the axes(x, y) without it(Phi in this case).
According to the sketch I provided, the Arctangent of Phi is the ratio between y/x, so clearly, they're interdependent.
If there any light you can shed on how I may actually trivialize the problem, but still maintain a direct solution for X and y, that will be most appreciated; A simple solution via r is something I would hope to avoid at this point, if you reckon it's possible.
As for the initial conditions, are there any suggestion what might be best plugged in just to verify the answer? I've tried nearly every possible value, in the vain hope of obtaining something plausible.
Grateful,
Daniel

 

[Philip Wood]

I'm not really addressing your problem head-on, but since you want to work in cartesians, let's get rid of r and phi. First phi...
m\ddot{x} = -\frac{K}{r^2}\frac{x}{r}
m\ddot{y} = -\frac{K}{r^2}\frac{y}{r}
in which r = (x^2 + y^2)^{1/2}

Well, there you are: two really nasty-looking coupled second order DEs. I'd solve them by going into polars...

 

[danielakkerma]

Hey!
Thanks for being so descriptive!
Could you please elaborate on how you've reached the minus signs there, in x/r;
Sadly, these equation(which I've already obtained), get me no further :(... I pretty much end up getting the same results. I continue to avoid transitioning to polars, still bent on getting a DE system for both X, Y, and since I am solving them numerically, an analytical solution doesn't worry me at present.
Where am I going wrong here?
Thank you very again,
Daniel

 

[Philip Wood]

My bit about going into polars was tongue-in-cheek!

To see where the minus signs come in, sketch an elliptical path with the Sun at one focus, at the origin of your co-ordinates. Take a point on your ellipse in the first quadrant. The Sun has components of its pull which are positive in the -x and -y directions, does it not?

Now the problem of initial velocity. I'd try one you know should work. Do some simple circular orbit theory and find the v for a given r, consistent with your value of K. I'll spell this out in more detail if I've been too cryptic.

 

[danielakkerma]

Some progress folks!
Ultimately, due to your indefatigable aid, I've managed to work out the majority of the issues, especially those concerning the signs, and arrived at a very dainty orbit(an elliptical one), albeit a precessing one, which I must verify if it is physically sound under my presents(see the (x, y, z) graph attached).
One query still unresolved, in my mind at least, but I am sure you could work it out in a jiffy, is the nature of the initial conditions.
I've already stated that, in my system, I've taken:
<br /> r(0) = x_0\hat{x}+y_0\hat{y}+0\hat{z}<br />
And v(0) =
<br /> v(0) = v^x_0\hat{x}+v^y_0\hat{y}+0\hat{z}<br />
In this configuration, naturally, L(the angular momentum is conserved, no doubt about that).
Now here's the problem, I've decided that I wanted to supply a tangential velocity only, meaning,
<br /> {v_t}^2= \frac{|\vec{r}\times{\vec{v}}|^2}{|r|^2} = \frac{...}{x0^2+y0^2} = {V_t}^2<br />
Here I set my v_t to my desired value,
But also demand that the radial velocity remain strictly zero(as is consistent with circular motion)
<br /> {v_r}^2= \frac{(\vec{r}\cdot\vec{v})^2}{|r|^2} = 0
[/itex]
The question is, how do I correlate between my values of K and m(which are the elements of the force), with the tangential velocity I am to give, in order to obtain circular motion(for instance)...
Obviously, there ought to be some dependence in the form of a centripetal force, i.e F(r0) = mv^2/r0, but here v has components which are difficult to extract. Is there a more sensible way of getting this initial transverse velocity? I rely on my algorithm(as is expected), after setting these conditions, to continue the computations and follow up on the path, but the boundary values are very irksome so far.
Again, I cannot thank you enough for all your inestimable help and assistance,
And with your suggestion, I can feel success in sight!
Thank you!
Daniel

 

[danielakkerma]

I've also attached(and finally achieved!), a circular trajectory generated at long last!
However, there's still the matter of these osscilations around the path which are unclear.
Can you shed some light on that?
Thanks!
Daniel

 

[Philip Wood]

Well done!
I suspect you're looking for something deeper than this, but the naive answer to your question about correlating v and K for a circular orbit is
v =\sqrt{\frac{K}{r}}
in which K = GM. M is the Sun's mass. The planet's mass has cancelled, because of the dual inertial and gravitational role of mass in Newtonian physics.

As for the slippage of the orbit, could this just be a cumulative numerical rounding error? You've probably realized that I've no experience at all of numerical methods, so have huge respect for your perseverance!

 

[danielakkerma]

Well guys, with your determination and steering, I've finally done it! It's been solved, and works like a charm...
Thank you so much for your patience and guidance here, it's been immeasurable and vital every step of the way. Thank you!
Humbled, and honored,
Daniel