SUMMARY
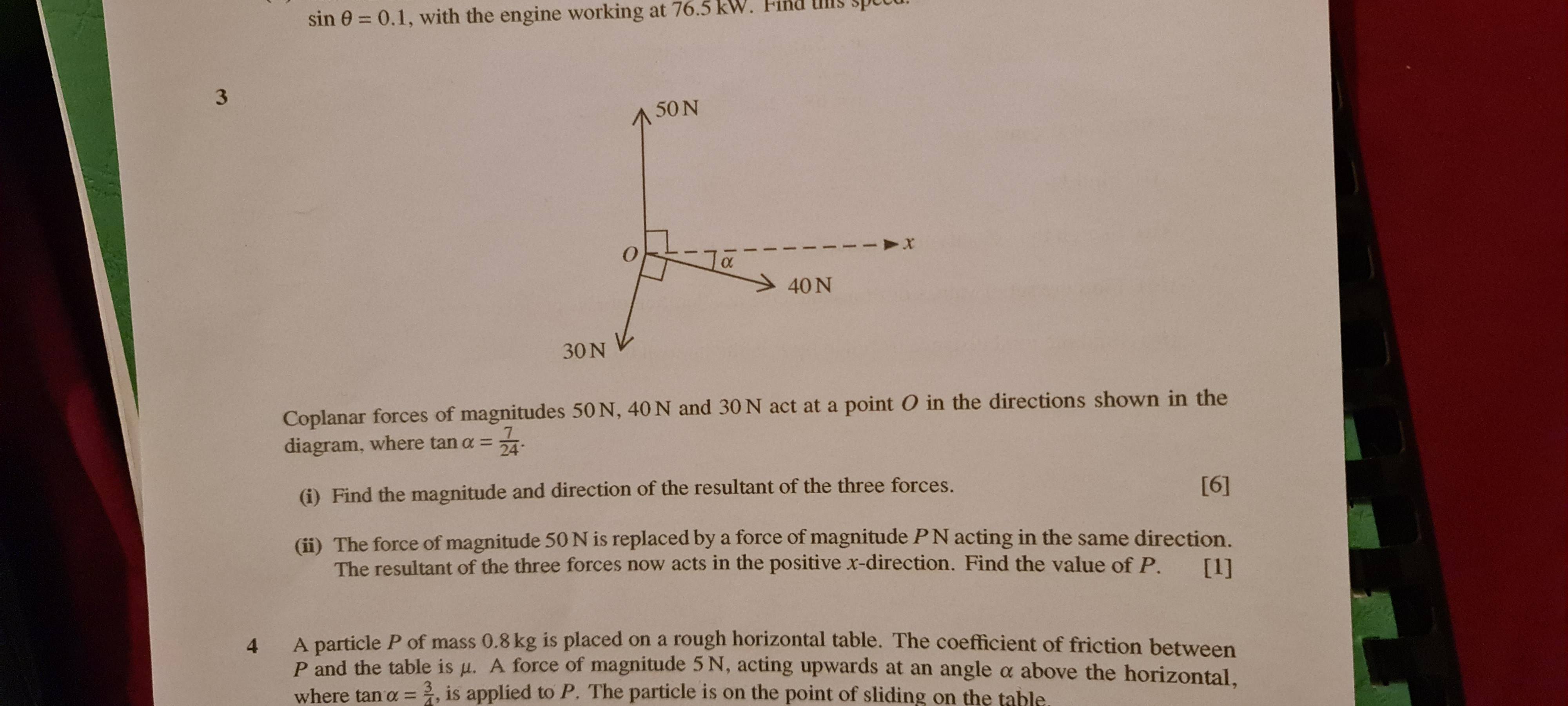
The discussion focuses on solving a mechanics problem involving the calculation of forces using vector components. The key forces mentioned are 40 N and 30 N, with components calculated as F(x) = 40cos(α) - 30cos(α) and F(y) = 40sin(α) - 30sin(α). The forces are confirmed to be coplanar, allowing for the use of the equations for net force and angle calculation: |F_net| = √((ΣF_x)² + (ΣF_y)²) and θ = arctan(ΣF_y/ΣF_x). The participants clarify the importance of focusing on x and y components due to the coplanarity of the forces.
PREREQUISITES
- Understanding of vector addition in physics
- Familiarity with trigonometric functions (sine and cosine)
- Knowledge of force components in mechanics
- Basic proficiency in solving equations involving square roots and arctangents
NEXT STEPS
- Study vector addition techniques in physics
- Learn about coplanar forces and their implications
- Explore the use of trigonometric identities in force calculations
- Practice problems involving net force and angle determination
USEFUL FOR
Students studying A-level mechanics, physics educators, and anyone seeking to improve their understanding of vector forces and calculations in mechanics.