A little different RC circuit problem Help

[juicec]

Homework Statement

First off, thanks for taking a look at my problem guys. I have been given this question as extra credit for a calc-physics II class and at the moment am struggling with pulling the pieces together. At first glance I didn't have to much trouble with it but when I go back to it to write it up, it begins to make less and less sense. We didn't really do a whole lot of RC circuit stuff in this summer term which is why I think in part he gave us this question, so I'm really just here to get some confirmation, some help and a little advice where ever possible.

So here it goes:

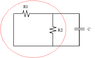
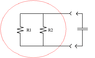
Find the time constant and the explicit time dependence for all currents. Assume that the capacitor is initially uncharged when switch S is closed. Make plots of the currents clearly indicating any features characteristic of the system.

You can view the diagram/full question here: http://www.scribd.com/doc/59234592/Problem-2

Homework Equations

We've got the charging/discharging formulas for RC circuits.
tao = RC
Series/parallel relationships.

The Attempt at a Solution

The plots are not an issue for me, the jist of it would be that at t=0, the capacitor drains all the current from the circuit, and the current exponentially decreases to infinity. At the same time the charge will have an exponential increase to a plateau.

My real issue stems from being unable to identify with reducing the circuit down into an effective resistance. When trying to calculate the time constants, for example where it goes from Battery -> R1 -> R2 -> battery, it is clear that R2 and C are in parallel, but at the same time R1 is in series to R2C. So I am thinking do we use the 1/jwc (resistance of a capacitor. We haven't actually learned this yet but I've read it online) and reduce the circuit into an effective resistance as you would any other regular R or C circuits. Basically what it comes down to is if someone could help me with one of the loops, I think I could take it from there. I am just unsure what exactly is our resistance and what exactly is our capacitance and how does the effective circuits come into play.

Again I am new to RC circuits in general but have a solid understanding of your basic R and C circuits.

Thanks in advance for any help provided, I'm under a pretty tight deadline and hope to hear from someone soon :)

 

[gneill]

Hi juicec, welcome to Physics Forums.

What circuit laws have you learned? Have you done any work with Thevenin or Norton equivalent circuits?

 

[juicec]

Hi juicec, welcome to Physics Forums.

What circuit laws have you learned? Have you done any work with Thevenin or Norton equivalent circuits?

To my knowledge we haven't learned either, but its possible the names just weren't brought up.

As far as circuit laws... Not sure exactly what this entails but, when in series additive, when in parallel inversely proportional, etc.

I think I'm simply over thinking this problem and I feel confident I can do it, just need a little kick to get started on the right track.

 

[gneill]

The tricky bit is going to be establishing the resistance to use for the time constant without resorting to solving the circuit's differential equation ("bone knives and bearskins" ). Or is this what you are expected to do?

 

[juicec]

I actually took differential equations but no we are not doing that in this class. From my best guess we are to reduce the circuit into the effective resistance and move on from there.

Finding tao = RC sounds pretty simple and straight forward but I am having a hard time getting started.

 

[gneill]

Okay. Well, to cut to the chase, one method of finding the equivalent resistance for a circuit is to "suppress" all sources (voltage and current sources) and then use the usual resistance combination formulas on the remaining network. To suppress a voltage source it is replaced in the circuit by a short circuit -- a wire. To suppress a current source, simply remove it entirely from the circuit.

In the present case you're looking for the resistance that the capacitor "sees" when it looks back towards the voltage source. So (temporarily) remove the capacitor, suppress the voltage source, and determine the resistance presented at the connections where the capacitor was.

 

[juicec]

OK, so just to let you know off the get go, I don't overly enjoy physics -_- Although I tend to do well in it, I do what's required and never go beyond. With that said, I am in physics II and haven't explored much past it.

So I can relate a bit better, isolating the example of Battery --> R1 --> R2 --> Battery:

If we wanted to find RC, you're suggested to remove the capacitor from the equation, find the effective resistance and reestablish the capacitor afterwords? I'm not sure what's going on here.

 

[gneill]

OK, so just to let you know off the get go, I don't overly enjoy physics -_- Although I tend to do well in it, I do what's required and never go beyond. With that said, I am in physics II and haven't explored much past it.

So I can relate a bit better, isolating the example of Battery --> R1 --> R2 --> Battery:

If we wanted to find RC, you're suggested to remove the capacitor from the equation, find the effective resistance and reestablish the capacitor afterwords? I'm not sure what's going on here.

The time constant for the circuit will depend in some fashion on BOTH resistances. In order to establish what that dependence is, we need to find the equivalent resistance that the capacitor "sees" .

Perhaps a slightly different way of looking at would help. Suppose that the capacitor had finished charging up (some long time after the switch closure). Now suddenly the voltage supply were removed and replaced by wire. The capacitor would begin to discharge. What would be the time constant for that circuit?

 

[juicec]

Using the same diagram, the capacitor would just discharge through R2 and C.

So the time constant when discharging would simply be tao = R2C ?

 

[juicec]

Oh your not saying open the switch, so the capacitor also discharges across R1, eh, again confused.

 

[gneill]

Oh your not saying open the switch, so the capacitor also discharges across R1, eh, again confused.

Correct

The capacitor discharges through BOTH resistors. What's the equivalent resistance that the capacitor sees?

 

[juicec]

Well I'm not to sure, don't we separate into different loops?

So it sees R1 in one situation and R2 in another, I am not sure how to do the effective resistance in this situation.

 

[gneill]

Would you say that the resistors are in series or in parallel?

 

[juicec]

well this I think is my problem, and perhaps after you help me out here I will be good to go. I thought that R2 and C are in parallel, but R1 and R2C are in series.

So perhaps I just answered my own question, the effective resistance is therefore in series? But the current still undergoes a junction, but then again capacitor holds no resistance... hm.

 

[gneill]

Let me redraw the circuit one more time. Are the resistors in series or in parallel? What will the capacitor see?

 

[juicec]

lol I feel like we are beating this to death here, but still so foggy :(

The resisters are now in parallel, the capacitor will have its current split across both?

 

[gneill]

lol I feel like we are beating this to death here, but still so foggy :(

The resisters are now in parallel,

Yes
Note that all the connections are still the same -- it's not a different circuit. Nothing changed but the way the circuit was drawn in order to make the relationship between R1 and R2 more obvious.

the capacitor will have its current split across both?

Yes

So the equivalent resistance that the capacitor "sees" is R1 in parallel with R2. That's the resistance that will go into the time constant.

 

[juicec]

OK so with resisters in parallel we simply find: R(eff) = R1 + R2.

So for the time constant of discharging with the battery removed at 100% charge,

tao = (R1 + R2)(C) ?

 

[gneill]

OK so with resisters in parallel we simply find: R(eff) = R1 + R2.

So for the time constant of discharging with the battery removed at 100% charge,

tao = (R1 + R2)(C) ?

R1 + R2 is for resistors in series (they add up). What's the formula for combining resistors in parallel?

 

[juicec]

Woops...

So its, R(eff) = (1/R1 + 1/R2)^-1(C)

which in turn gives us ((R2+R1)/R1R2)^-1(C)

which in turn gives us [(R1R2)/(R1+R2)](C)?

 

[gneill]

Woops...

So its, R(eff) = (1/R1 + 1/R2)^-1(C)

which in turn gives us ((R2+R1)/R1R2)^-1(C)

which in turn gives us [(R1R2)/(R1+R2)](C)?

Yes

So now you have the time constant for the circuit. It'll apply to all the exponential functions for the circuit. What's your next step?

 

[juicec]

ok so that's the time constant of the circuit without the battery and the switch closed right? Does the time constant not change?

For example, would the time constant be different if the switch was open and the capacitor was discharging? Because in that case it would just be discharging across the R1?

 

[gneill]

ok so that's the time constant of the circuit without the battery and the switch closed right? Does the time constant not change?

For example, would the time constant be different if the switch was open and the capacitor was discharging? Because in that case it would just be discharging across the R1?

Yes, as you surmise the time constant is different when the switch is open (Just R1 applies, as you say). But from what I can tell for the given problem, the switch is initially open, then it's closed at time t=0 and remains closed thereafter.

 

[juicec]

Yes, OK, so if you read the problem one more time... I would have 2 time constants, one when the switch is closed which we have now found above, and one when it is open where the capacitor is discharging into R2 which I would venture a guess at it simply being:

tao = (R2)(C) ?

 

[gneill]

Yes, OK, so if you read the problem one more time... I would have 2 time constants, one when the switch is closed which we have now found above, and one when it is open where the capacitor is discharging into R2 which I would venture a guess at it simply being:

tao = (R2)(C) ?

Sure. Looks good.

 

[juicec]

OK, I'll take that as a, "awsome! perfect!" ;) lol

OK so now with the time constants in toe, how do we attack the "explicit time dependence for all currents" ?

 

[juicec]

Thinking about it now... would it be a matter of subbing in our time constant into a charging/discharing equation and calling it a day?

 

[gneill]

OK, I'll take that as a, "awsome! perfect!" ;) lol

OK so now with the time constants in toe, how do we attack the "explicit time dependence for all currents" ?

The practical approach is to ascertain the starting and ending values for each current and then just bung in an exponential function to achieve the transition. Hardly any circuit analysis required!

For example, you know that the capacitor will initially have zero volts on it, and so it'll look like a short circuit across R2 the instant after the switch is closed. What's the initial current going to be through the capacitor (hint: what is limiting it?).

When the capacitor is fully charged, what's the current through it?

 

[juicec]

Initially only R1 is limiting what is going through the capacitor right?

When the capacitor is fully charged, eh, I should probably know these answers but it would simply be I going through it since there is no resistance when its fully charged? -- Or does the capacitor "close" when its fully charged? I thought I remembered hearing that somewhere

 

[gneill]

Initially only R1 is limiting what is going through the capacitor right?

Right.

When the capacitor is fully charged, eh, I should probably know these answers but it would simply be I going through it since there is no resistance when its fully charged? -- Or does the capacitor "close" when its fully charged? I thought I remembered hearing that somewhere

An initially discharged capacitor behaves like a short circuit in the first instant.

After steady state is achieved, the current through a capacitor is zero: it looks like an open circuit.

 

[gneill]

...so what are the initial and final values for the current through the capacitor?

 

[juicec]

ah OK, interesting. So with that said now, we've got 2 time constants, and also 2 circuits? One for discharging and one for charging. Or in fact we have 4 circuits, 2 when charging (capacitor empty/full) and 2 when discharging (capacitor full/empty).

 

[juicec]

...so what are the initial and final values for the current through the capacitor?

I'm not 100% sure how to answer this.

 

[juicec]

Unfortunately I have to sign off for the evening, I will look forward to continuing this tomorrow hopefully. I am almost there :) Perhaps with a fresh mind and a bit of scrap paper I can finish this off and report the findings to you tomorrow.

Thanks again for all the help. I have been trying to find some assistance with this for weeks and within minutes of posting here I got a detailed answer and a great tutor! :)

Thanks again, truly appreciate all your help.

All the best.