A potential well with 3-fold reflection symmetry

In summary, Bloch's theorem and the tight-binding approximation can be used to find eigenstates of a system. However, applying it to a specific case can be confusing. Bloch's theorem states that a wavefunction can be represented as a product of a plane wave and a periodic function. It would be helpful to have a discussion to guide thinking and provide assistance with the homework. Any comments or suggestions would be greatly appreciated.
  • #1
lazayama
5
0
Homework Statement
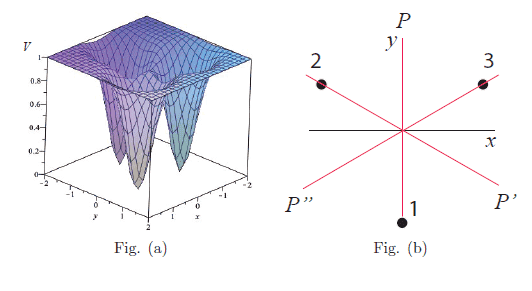
Photos are attached below, with figures
Relevant Equations
Bloch's theorem: $$\psi(r)=e^{ikr}u(r)$$
Simultaneous eigenstates of Hamiltonian and Translational operator: $$|\theta>=\Sigma_{n=0} ^{N-1}|n>*e^{in\theta} $$
When we are talking about Bloch's theorem and also the tight-binding approximation, we can use them to help finding eigenstates of a system. However, I am so confused how to apply it in this case (below is my homework) and don't even know how to start it...

All I understand about the Bloch's theorem is that we can find a wavefunction that is a product of plane wave and a periodic function.

This will be great if someone can discuss it with me and direct my thinking...This may be a silly question but I am really lost here... I am not asking for direct answer but I really need a hand on this, so a solid discussion would be really helpful.

Thanks in advance!

Untitled.png

Untitled2.png
 
Physics news on Phys.org
  • #2
Any comments or suggestions would be highly appreciated, really!
 

1. What is a potential well with 3-fold reflection symmetry?

A potential well with 3-fold reflection symmetry is a type of energy well in which the potential energy function has a 3-fold rotational symmetry and is also symmetric under reflection across three different planes. This results in a well with three identical minima where a particle can be trapped.

2. How is a potential well with 3-fold reflection symmetry different from other types of potential wells?

A potential well with 3-fold reflection symmetry is unique in that it has three identical minima, whereas other types of potential wells may have different depths or shapes for each minimum. Additionally, the symmetry of the potential energy function in a 3-fold reflection symmetric well allows for certain symmetries in the wave function of a trapped particle.

3. What are some real-world examples of potential wells with 3-fold reflection symmetry?

One example of a potential well with 3-fold reflection symmetry is a molecule with three identical atoms arranged in an equilateral triangle. The potential energy function for the molecule would have three identical minima at the locations of the atoms. Another example is a crystal lattice with three identical atoms in the unit cell, resulting in a potential well with three-fold reflection symmetry.

4. How is the energy of a particle trapped in a potential well with 3-fold reflection symmetry affected by its position?

The energy of a particle trapped in a potential well with 3-fold reflection symmetry is affected by its position in the well. The particle will have the lowest energy when it is located at one of the three minima, and the energy will increase as it moves away from these points. The energy levels of the particle will also exhibit certain symmetries due to the symmetry of the potential energy function.

5. What are the applications of potential wells with 3-fold reflection symmetry?

Potential wells with 3-fold reflection symmetry have various applications in physics and chemistry. They can be used to model the behavior of molecules and crystals, as well as in the study of quantum mechanics. Additionally, they have practical applications in technologies such as semiconductors and lasers, where the symmetries of the potential well can affect the properties of the materials.

Similar threads

Average value of the impulse as the parameters vary
    • Advanced Physics Homework Help
Replies
14
Views
876
Calculating the Fraction of Time Particles Spend Outside a Potential Well
    • Advanced Physics Homework Help
Replies
16
Views
3K
I Bloch Waves within Tight Binding Approximation
    • Atomic and Condensed Matter
Replies
1
Views
1K
Electron distribution using tight binding band structure?
    • Atomic and Condensed Matter
Replies
1
Views
1K
How Do Parity and Potential Affect Quantum Well Solutions?
    • Advanced Physics Homework Help
Replies
2
Views
1K
MHB The Integers as an Ordered Integral Domain .... Bloch Theorem 1.4.6 ....
    • Topology and Analysis
Replies
4
Views
1K
Model with SU(2) gauge symmetry and SO(3) global symmetry
    • Advanced Physics Homework Help
Replies
1
Views
1K
'Symmetry argument' for eigenstate superposition
    • Advanced Physics Homework Help
Replies
3
Views
1K
Standard Finite Well Problem (Solve without symmetry)
    • Advanced Physics Homework Help
Replies
1
Views
3K
Crystal momentum in a lattice.
    • Atomic and Condensed Matter
Replies
6
Views
4K

Hot Threads

Recent Insights

Back
Top