A problem in solving Schrodinger equation for hydrogen

[patric44]

Homework Statement

iam having a little problem related to solving the theta part for the hydrogen atom

Relevant Equations

problem with the theta part of the SE and associated Legendre function

hi guys
i am having a little problem concerning the theta part of TISE :

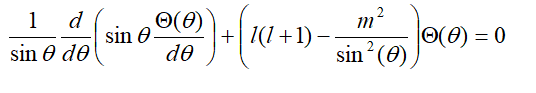
its clearly that its very similer to the associated Legendre function :

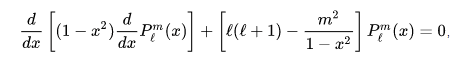
how iam going to change 1/sinθ ... to (1-x^2) in which x = cosθ
i tried many identities but i am stuck here .
any help on that ?

 

[mitochan]

Hi.
Try substitute
\frac{d}{d\theta}=\frac{dx}{d\theta}\frac{d}{dx}=-sin\theta\frac{d}{dx}