A specific case of an exception to Archimedes' Principle?

[Novus]

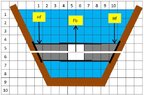
That is straightforward as long as one makes the assumption that the trapezium moves slowly enough that the fluid remains at approximate equilibrium at all times.

The fluid is free to flow up and down past the trapezium. So Pascal's principle applies. Pressure is given by $P = \rho g h$. The total force on the top and bottom surface is easily calculated: $F=PA$. The difference between those forces is the net force on the trapezium. We can ignore the forces on the slanted faces on the right and left because those are both zero. We can ignore the forces on the flat faces on the front and back because those cancel with each other.

This would than be the same calculation as per my suggestion in post 26 I believe.

 

[A.T.]

This would than be the same calculation as per my suggestion in post 26 I believe.

Yes, but note that's it's not enough to show positive buoyancy. In order for the object to rise, the buoyancy also has to be greater than the weight of the object.

 

[A.T.]

If these calculations are correct P.E. will decrease with an upwards motion of the trapezium shaped object.

Makes sense to me. When air bubbles rise they also expand and so does the water level, but the total PE of the water decreases.

 

[Novus]

Yes, but note that's it's not enough to show positive buoyancy. In order for the object to rise, the buoyancy also has to be greater than the weight of the object.

In post 26 I calculated positive Fb for both scenarios. In addition, as per the original description, the object consists of solid area's with the same density as water and a 'pocket' of air, therefore the overall density of the object will be less than the density of the surrounding water. I'm still uncertain if the object will move up or down, you're example of air bubbles rising and expanding doesn't apply here I believe, since the bubbles expand as a result of a higher initial internal pressure. In the scenario being discussed the air volume is directly connected to the outside ambient air and therefore will maintain the same pressure when moving up or down.

 

[A.T.]

Yes, but note that's it's not enough to show positive buoyancy. In order for the object to rise, the buoyancy also has to be greater than the weight of the object.

In post 26 I calculated positive Fb for both scenarios. In addition, as per the original description, the object consists of solid area's with the same density as water and a 'pocket' of air, therefore the overall density of the object will be less than the density of the surrounding water.

Lower density doesn't necessarily mean it will rise, because not all sides are subject to hydrostatic pressure. If you do the force analysis, you add up all forces, including weight, and look at the direction of the net force. Comparing densities is not part of that analysis.

you're example of air bubbles rising and expanding doesn't apply here I believe,

I didn't mean to imply it's exactly the same. It's just a more natural example which shows that raising the water level doesn't imply increasing the water's PE.

Note the in the energy analysis you also have to take the change of the object's PE into account as well. The total PE energy of water and object must decrease.

 

[pbuk]

Just because the water level rises, doesn't necessarily mean that the water's center of mass (and thus PE) also rises.

That is an excellent point, and the rising air bubble is a perfect illustration. I think intuition is misleading here, and short-cuts don't work: calculating the forces is the reliable way to solve it.

 

[Novus]

Lower density doesn't necessarily mean it will rise, because not all sides are subject to hydrostatic pressure. If you do the force analysis, you add up all forces, including weight, and look at the direction of the net force. Comparing densities is not part of that analysis.

To summarize what has been concluded so far;

Post 25 - 'Because the object is not surrounded by fluid on all sides, Archimedes law does not apply. The net force from fluid pressure must be calculated from first principles rather than from the weight of the displaced fluid.'

Post 25 - 'I agree that there are no lateral forces. And no vertical forces from the sealed and slanting sides.
Post 26 - according to my calculations the P.E. of the water will decrease when the object rises and increases in volume.

'To add up all forces including weight' would include the forces on the triangular slanted area's, which are possibly similar to the bottomcase exception to the AP, which may not be that straithforward;

https://file.scirp.org/Html/1-1720827_75679.htm A question that normally comes up during discussions of Archimedes’ principle is that when an object in the form of a rectangular block rests on the bottom of a container with no fluid under it, where does the upward buoyant force come from? In fact, in this case because of the fluid pressure on top of the block, the net hydrostatic force on it would be downward, resulting in the apparent weight of the block to be greater than its true weight. But this conclusion is in complete contradiction with all observations since even in this case the apparent weight of the block is less than its true weight by the weight of the fluid displaced.

https://www.researchgate.net/publication/51958652_Using_surface_integrals_for_checking_Archimedes'_law_of_buoyancy

However, this law, also known as Archimedes’ principle (AP), does not yield the force observed when the body is in contact to the container walls, as is more evident in the case of a block immersed in a liquid and in contact to the bottom, in which a downward force that increases with depth is observed I could make an attempt based on dissecting the trapezium in 3 area's - applying the standard AP to the rectangular middle section and applying a force analysis on the 2 triangular area's as per the bottom case exception?

I didn't mean to imply it's exactly the same. It's just a more natural example which shows that raising the water level doesn't imply increasing the water's PE.

Note the in the energy analysis you also have to take the change of the object's PE into account as well. The total PE energy of water and object must decrease.

Attached 'Waterbubble.jpg' - comparing energy input required to push a volume to the bottom of a liquid with the resulting P.E. at the bottom position - includes 3 scenario's;
1. A rigid volume of air where we need to excert a vertical downwards energy to push the object to the bottom where it will have gained an equal amount of P.E. 2. The same object but now with sides which can be compressed. As a result less vertical downward energy will be required to push the object to the bottom (as a result the air volume will be compressed by increasing waterpressure) and less upward P.E. will haven been gained than in example 1 (if we ignore the P.E. of the compressed air volume) 3. Would be similar to scenario 2 (same amount of energy input required to arrive at an identical P.E.?) except for the fact that in this case the volume of air is not changed by waterpressure?

 

[Bystander]

You trying to build a "PPM/over-unity device?" Es ist verboten. See "Forum Rules." There was a "bubble power tower" discussion somewhere on the forum ...been long enough in the past that search fails/ed....

 

[A.T.]

'To add up all forces including weight' would include the forces on the triangular slanted area's, which are possibly similar to the bottomcase exception to the AP, which may not be that straithforward;

Yes, but you could add up all the other forces, to find the slanted area forces needed to hold the object in place. That will tell which way the object will move, if you would actually be able to build that sliding sealed contact with negligible friction.

 

[Novus]

You trying to build a "PPM/over-unity device?" Es ist verboten. See "Forum Rules." There was a "bubble power tower" discussion somewhere on the forum ...been long enough in the past that search fails/ed....

The laws of thermodynamics and the law of conservation of energy are important fundamental laws of physics in general.

A perpetual motion machine is therefore impossible, as it would violate either the first or second law of thermodynamics.

As I already explained I became interested in the exceptions to the A.P. after which I made some sketches. Purely from a theoretical standpoint I was unable to answer the question which forces where at play in the topic question. (note that I' ve no intention to build anything)

In post 24 I provided an example on how the object could move up or down only because I was challenged to think about this as a result of the questions in the earlier posts (for example 4 and 21)

Not sure how this related to 'waterbubbles' (or a 'bubble power tower') which was initially brought up by A.T. as an example whereby an increase in airvolume of a submerged object does not neccesarily result in an increase of the P.E. of the watervolume?

I believe this topic deserves merit since (i) buoyancy concepts are in some cases poorly understood by undergraduate students (https://www.researchgate.net/publication/269212621_Exploring_Student_Difficulties_with_Buoyancy) (ii) until recently there were still debates within the scientific community on the forces at play for the bottomcase scenario (https://www.scielo.br/j/rbef/a/w7VfCBmYgN46Wm77ttMmQ7d/?lang=en) (iii) the discussions in the links I provided on the question if/how the wording of the AP can be altered to incorporate the bottom- and side case exceptions.

 

[Novus]

Yes, but you could add up all the other forces, to find the slanted area forces needed to hold the object in place. That will tell which way the object will move, if you would actually be able to build that sliding sealed contact with negligible friction.

I do not intend to build anything. Solving Fb for the total volume of the object (note that in this case calculating Fb as the difference between the top and bottom area does not work); Fb = V * p * g = 18 cm3 * 1 kg/m3 * 9.81 m/s2 = 0.1766 N. For the downwards hydrostatic force on top of the slanted area's; Hf = p* g * h * A = 1 kg/m3 * 9.81 m/s2* 4 cm * 2 cm2 = 0.0785 N. The resulting Fb(res) = Fb - Hf = 0.0981 N. W = m * g = 0.014 kg* 9.81 m/s2 = 0.1373 N. The object will therefore move in a downwards direction. Unless there are any further questions this topic can therefore be closed. I would like to thank the advisors on this forum (especially A.T.) for their patience and guidance resulting in a learning curve on my part.