Drag equation - relative flow velocity

[axim]

Hello!
I have a question about aerodynamic drag. It sounds simple but when trying to understand why the relative velocity can be used in calculations I have some trouble. The formula is 0.5*rho*u²*cd*A where u is the relative velocity between the object and the fluid. The cd value depends on the shape. For sake of simplicity let it be 1 in the example.

For an object object moving trough a liquid (air) which is not moving, there is often a simplified explanation in textbooks.
If the object moves at a speed v1, it displaces air in front of it. In the time t1 a specific mass of air is pushed away. The mass can be easily calculated by v1*t1*A*density. v1*t1 is the distance passed, A the area and rho the density, so I know the displaced volume and with that the mass.
So for velocity v1 the air is accelerated and gains the kinetic energy of 0.5*m1*v1². Of course this is simplified because the flow is more complicated.
Now let's say I triple the speed. Then the object will travel through 3 times the mass and it will be accelerated to 3 times the speed. According to the drag force formula I need a force 9 times higher due to the u². This is also understandable and explainable with this model: I will accelerate 3*m1 to (3*v1)² so I have 27 times the energy of 0.5*m1*v1²: (0.5*3*m1*(3*v1)²) but I also have traveled 3 times the distance, so I can see the force required is 9 times higher (as expected for triple speed) and force*distance went into the kinetic energy of the air (and will finally end up as friction after later the movement has calmed down).

Everything fine so far. Now I have trouble to imagine how and where the energy is going when using a relative velocity.
Instead of the object moving at 3*v1, let's now say the object is moving at 2*v1 and there is a headwind with the speed -1*v1.
As the relative speed is used in the formula, the object will experience the same drag force: 0.5*rho*(2*v1-(-v1))²*A=0.5*rho*(3*v1)²*A.
Now, I try to find out how and where the energy "goes". And this is where I have trouble with this simplified model.

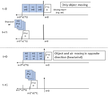
The object is moving at 2*v1, the air is approaching it with -1*v1. This means, the object will again displace three mass-units (3*m1) of air: It will move less distance 2*v1*t1, but meanwhile the air will travel -1*v1*t1 in direction of the object, so it was in contact with the same amount (3*m1) of air during t1. I created a small drawing so my explanation is not too confusing.
Then I tried to calculate it worst case: Every collision is inelastic, the air slows down the object. Then the object has to accelerate itself and the air to the speed of 2*v1 again. I always end up with the result that less work is required to travel the same distance and push away the air compared to the first example (I also considered that with v=2*v1 the object travels less distance during t1). If requested I can detail my calculations but I think it leads in the wrong direction.So this simplified Newtonian approach can't explain that I can use the relative speed in the formula.
I did also try to get the basics from transport phenomena lectures or explanations about the Navier Stokes equations but I end up with very complex mathematical derivations (I don't doubt these are correct), but still I miss the rough idea why I can just use the relative speed. The formulas with stress tensors just get too complex to grasp how the movement is going on. The transport phenomena explanations also usually touch the molecular level.

Is there any simplified model that can picture why the relative speed can be used if the object and fluid are moving?
Especially how the spent work relates to the kinetic energy changes and friction compared in the two examples: Relative speed is the same, but in one case only the object is moving, in the other case the object and fluid are moving in opposite direction.

Thanks in advance

 

[Chestermiller]

If they are moving at constant speeds,, then you can adopt a frame of reference with the object is stationary. Does this help simplify the situation?

 

[jbriggs444]

Energy is conserved. But it is not invariant.

Conserved: Once you pick a reference frame and stick with that reference frame, energy is conserved.

Invariant: If you change from one reference frame to another, the total energy remains the same (it actually will not).

It is not just energy that is not invariant. Work is also not invariant.

If you adopt a frame where an object is stationary, you can ignore the work done by forces acting on the object. If you adopt a frame where the object is moving, you have to account for the work done by forces acting on the object.

 

[vanhees71]

Well, it depends. If you only look at the object moving under air resistance its energy is not conserved, because friction is a dissipative process. If you take into account the air including its internal energy, energy is of course conserved, and you have some heat production due to friction.

 

[Lnewqban]

How does the object and its energy “know” that you are measuring velocity respect to a far down surface of reference that they don’t even “see”?
The object could be stationary respect to ground, or even move backwards, if the fluid has enough kinetic energy.

 

[axim]

Energy is conserved. But it is not invariant.

Conserved: Once you pick a reference frame and stick with that reference frame, energy is conserved.

Invariant: If you change from one reference frame to another, the total energy remains the same (it actually will not).

It is not just energy that is not invariant. Work is also not invariant.

If you adopt a frame where an object is stationary, you can ignore the work done by forces acting on the object. If you adopt a frame where the object is moving, you have to account for the work done by forces acting on the object.

Thanks for the fast reply. I tried it but get different results in the required work.
I need help with that concept of the reference frame and the conserved work.

I will explain what I calculated, maybe that way you can see what I get wrong.
To get your point I think we could forget about the air and just imagine it as 1kg blocks for each m³.

To simplify the calculation I will assume an air density of 1kg/m³ instead of 1.225, or just one mass element.
The object should also have a mass of 1kg.
Reference frame 1 (top example):
The object has a speed of 3m/s. The air has a speed of 0m/s. The object hits the first m³ (1kg) of air.
Speed of object before: 3m/s. Total impulse before: 1kg*3m/s+1kg*0m/s=3kg*m/s
After inelastic collision: Impulse has to be the same, hence speed of object and speed of first m³ of air: 1.5m/s (3kg*m/s=(1kg+1kg)*v).
Kinetic energy before: 0.5*1kg*(3m/s)²=4.5Nm
Kinetic energy of the system after collision: 0.5*(1kg+1kg)*(1.5m/s)²=2.25Nm -> Energy lost in collision with first m³ of air: 2.25Nm (4.5Nm-2.25Nm)
Kinetic energy when object and 1kg of air are accelerated back to 3m/s: 0.5*(1kg+1kg)*(3m/s)^2=9Nm.
Work required to bring object and air to speed of 3m/s: 9Nm-2.25Nm=6.75Nm.
So to move 1m the energy of 6.75Nm was required to maintain the speed.
This repeats every meter as 1m³ of air is displaced. I assume the displaced air moves to the side with a negligible speed so it will not impact the other mass blocks ahead (again this is now not the fluid mechanics, just the concept of the reference frames I'm tring to get).
Having moved 2 meters 6.75*2=13.5Nm are required as two collisions will happen.

Reference frame 2 (lower example)
The object has a speed of 2m/s. The air has a speed of -1m/s. Same relative speed if I'm looking from the object's view. The object hits the first m³ (1kg) of air. I will switch to the outside observer:
Total impulse before: 1kg*2m/s+1kg*(-1m/s)=1kg*m/s. After inelastic collision: Speed of object and first m³ of air=0.5m/s
Kinetic energy before collision: 0.5*1kg*(2m/s)²+0.5*1kg*(-1m/s)²=2.5Nm
Kinetic energy after collision: 0.5*(1kg+1kg)*(0.5m/s)²=0.25Nm -> Energy lost in collision = 2.25 - same as in the other reference frame as expected, that was the part I unterstood so far about the reference frames!
Kinetic energy when object and 1kg of air are accelerated back to 2m/s (moving object should not be slowed down as in other reference frame): 0.5*(1kg+1kg)*(2m/s)²=4Nm
Work required: 4Nm-0.25Nm=3.75Nm.
While moving 2 meters, this collision and acceleration happens three times (see the drawing in the initial post). Why not two times? Because while the object is moving 2 meters, the air mass blocks are also moving so eventually there are three air blocks hitting the object.
Hence, I expect that the work required to move the object 2m is 3*3.75Nm=11.25Nm.

This is different from the result above where 13.5Nm are calculated.

What am I getting wrong here?

 

[jbriggs444]

Please forgive me as I try to follow along with your work, mumbling as I go.

Reference frame 1 (top example):
The object has a speed of 3m/s. The air has a speed of 0m/s. The object hits the first m³ (1kg) of air.

We are in the rest frame of the air. We have an object that is moving at 3 m/s. It must be propelled by some propulsive force, $F$. This propulsive force contributes power to the system at a rate of $3F$ watts.

Speed of object before: 3m/s. Total impulse before: 1kg*3m/s+1kg*0m/s=3kg*m/s

So we seem are trying to calculate F here. But no.

You write "impulse" when you mean "momentum". You are trying to invoke momentum conservation and have a 1 kg object slowing upon encountering 1kg of air in a completely inelastic collision.

Not the scenario I had in mind, but OK, we can roll with it. We have 1.5 kg m/s of rearward impulse applied to the object and 1.5 kg m/s of forward impulse applied to the air. Both end up moving at 1.5 m/s in the object's original direction of travel.

After inelastic collision: Impulse has to be the same, hence speed of object and speed of first m³ of air: 1.5m/s (3kg*m/s=(1kg+1kg)*v).

Yes.

Kinetic energy before: 0.5*1kg*(3m/s)²=4.5Nm

Sounds right.

Kinetic energy of the system after collision: 0.5*(1kg+1kg)*(1.5m/s)²=2.25Nm -> Energy lost in collision with first m³ of air: 2.25Nm (4.5Nm-2.25Nm)

Sounds right. We've lost half of our original KE in the inelastic collision.

Kinetic energy when object and 1kg of air are accelerated back to 3m/s: 0.5*(1kg+1kg)*(3m/s)^2=9Nm.

Yes, if we accelerate both back up to 3 m/s then we've doubled our initial KE

Work required to bring object and air to speed of 3m/s: 9Nm-2.25Nm=6.75Nm. So to move 1m the energy of 6.75Nm was required to maintain the speed.

Yes. So we've burned 2.25 J on thermal energy. 6.75 J on mechanical energy for a total of 9 J.
We've moved 1 meter and done 9 J of work. That is a force of 9 N.

The energy accounting adds up.

This repeats every meter as 1m³ of air is displaced. I assume the displaced air moves to the side with a negligible speed so it will not impact the other mass blocks ahead (again this is now not the fluid mechanics, just the concept of the reference frames I'm tring to get).
Having moved 2 meters 6.75*2=13.5Nm are required as two collisions will happen.

Nope. You've forgotten to count the 2.25 J going into thermal losses. You need work to support that.

Reference frame 2 (lower example)
The object has a speed of 2m/s. The air has a speed of -1m/s. Same relative speed if I'm looking from the object's view. The object hits the first m³ (1kg) of air. I will switch to the outside observer:

We know that the kinetic energy losses must tot up to 2.25 J this time as well. We just have to watch you do the math.

Total impulse before: 1kg*2m/s+1kg*(-1m/s)=1kg*m/s. After inelastic collision: Speed of object and first m³ of air=0.5m/s
Kinetic energy before collision: 0.5*1kg*(2m/s)²+0.5*1kg*(-1m/s)²=2.5Nm
Kinetic energy after collision: 0.5*(1kg+1kg)*(0.5m/s)²=0.25Nm -> Energy lost in collision = 2.25 - same as in the other reference frame as expected, that was the part I unterstood so far about the reference frames!

Yep. Perfect.

Kinetic energy when object and 1kg of air are accelerated back to 2m/s (moving object should not be slowed down as in other reference frame): 0.5*(1kg+1kg)*(2m/s)²=4Nm
Work required: 4Nm-0.25Nm=3.75Nm.

Plus the 2.25 J of thermal losses as before for a total of 6 J.

This time the object has only moved 2/3 of a meter because the air was oncoming and moved 1/3 of a meter. So we divide 6 by 2/3 yielding 9.

Voila. The predicted force is 9 N again.

If you do a momentum analysis, you'll arrive at the same predicted force of 9 N more easily.

 

[axim]

Please forgive me as I try to follow along with your work, mumbling as I go.

It's the best you can do to help me, I really appreciate you taking the time a lot! I guess others will also be thankful. Really glad you take time.

Reference frame 1 (top example):
The object has a speed of 3m/s. The air has a speed of 0m/s. The object hits the first m³ (1kg) of air.

We are in the rest frame of the air. We have an object that is moving at 3 m/s. It must be propelled by some propulsive force, $F$. This propulsive force contributes power to the system at a rate of $3F$ watts.So we seem are trying to calculate F here. But no.

You write "impulse" when you mean "momentum". You are trying to invoke momentum conservation and have a 1 kg object slowing upon encountering 1kg of air in a completely inelastic collision.
Not the scenario I had in mind, but OK, we can roll with it. We have 1.5 kg m/s of rearward impulse applied to the object and 1.5 kg m/s of forward impulse applied to the air. Both end up moving at 1.5 m/s in the object's original direction of travel.

Sorry, I account that to the translation! I realized what's called momentum in English (p, m*v) is called impulse here, and the impulse you're referring to (J, force over time) uses a different term!

After inelastic collision: Impulse has to be the same, hence speed of object and speed of first m³ of air: 1.5m/s (3kg*m/s=(1kg+1kg)*v).

Yes.

Kinetic energy before: 0.5*1kg*(3m/s)²=4.5Nm

Sounds right.

Kinetic energy of the system after collision: 0.5*(1kg+1kg)*(1.5m/s)²=2.25Nm -> Energy lost in collision with first m³ of air: 2.25Nm (4.5Nm-2.25Nm)

Sounds right. We've lost half of our original KE in the inelastic collision.

Kinetic energy when object and 1kg of air are accelerated back to 3m/s: 0.5*(1kg+1kg)*(3m/s)²=9Nm.

Yes, if we accelerate both back up to 3 m/s then we've doubled our initial KE

Work required to bring object and air to speed of 3m/s: 9Nm-2.25Nm=6.75Nm. So to move 1m the energy of 6.75Nm was required to maintain the speed.

Yes. So we've burned 2.25 J on thermal energy. 6.75 J on mechanical energy for a total of 9 J.
We've moved 1 meter and done 9 J of work. That is a force of 9 N.

The energy accounting adds up.

This repeats every meter as 1m³ of air is displaced. I assume the displaced air moves to the side with a negligible speed so it will not impact the other mass blocks ahead (again this is now not the fluid mechanics, just the concept of the reference frames I'm tring to get).
Having moved 2 meters 6.75*2=13.5Nm are required as two collisions will happen.

Nope. You've forgotten to count the 2.25 J going into thermal losses. You need work to support that.

Ok! Now I think we're coming to the crucial point where I have something different in mind! I think if we can clarify this my problem can be solved.

My expectation of what happens was: As the object hits the first m³ of air, as we calculated above, 2.25 J are dissipated into heat, and both the object and the air are moving at 1.5 m/s.

In my expectation there is no external force required in this action at all, it is just observing the collision. Only afterwards an external force is required to accelerate both objects again, but which requires only 6.75 Nm.
So the problem is I can't see where an external force is required to support the 2.25 J losses.

What I could imagine - but I'm not sure if it is correct to assume:
I will not wait until the collision is finished and then accelerate both masses again, I will continue moving the object at 3 m/s until the second mass (air) is also accelerated to 3 m/s. Here I'm missing of how that would look like in microscopic view for a solid block, but I imagine it for the following calculation as two object sliding over each other with friction.

When I calculate this there is a difference in losses leading to either your or my result:

Case A: If I just let the collision happen without an external force, the object will slow down, while the second mass is accelerated. Let's assume a friction of 15 N. Time to accelerate the air mass to 1.5 m/s: 0.1 s (15N/1kg=15m/s²). The air mass has moved 7.5 cm ((1.5m/s)/2*0.1s). Meanwhile the object has moved (3m/s-1.5m/s)/2*0.1s=22.5 cm. So it has slipped 22.5cm-7.5cm=15 cm over the mass, and heat energy of 0.15m*15N=2.25 J was dissipated. Matches my original expectation. Note: No external force was required so far. I only require 6.75Nm now to accelerate object + the air maiss again. But not 9Nm.

Case B:
I continuously keep the object moving at 3m/s until the second mass (air) is accelerated to 3m/s also. Again I'll use the friction of 15 N. To reach 3 m/s, the double time is required, 0.2 s. That means, the air mass has moved 0.5*15m/s²*(0.2s)²=0.3 m. The object has kept its speed so the external force required was 15 N. Meanwhile it has moved 3m/s*0.2s=0.6 m. Here it has slipped 0.6m-0.3m=0.3m. This means 0.3m*15N=4.5 J losses were generated! Higher than in case A. As the force was applied over 0.6 m this time 0.6m*15N=9 Nm were required! That is the number we were looking for. Difference: In this case there was more thermal loss due to more relative movement (object sliding over the second (air) mass) as I did not allow the object to slow down.

So those were quiet a lot of assumptions of what could happen to get the right numbers...
The difference is that in one case I let the collision and acceleration happen after each other, in the other case it happens continuously and the results are different.

Now the question is: What's correct to assume? What is the model/calculation you have in mind (as my original assumptions give me the wrong results)?
I think it's what you have in mind when you wrote "You've forgotten to count the 2.25 J going into thermal losses. You need work to support that." is what I'm missing currently.

Reference frame 2 (lower example)
[...]

I will calculate this again after the point above is clarified.

 

[jbriggs444]

In my expectation there is no external force required in this action at all, it is just observing the collision. Only afterwards an external force is required to accelerate both objects again, but which requires only 6.75 Nm.
So the problem is I can't see where an external force is required to support the 2.25 J losses.

I had the same difficulty until I slowly realized... We are doing an accounting for mechanical energy.

If one is going to account for [mechanical] energy and make sure that the books balance then one should account for energy and make sure that the books balance. There is an energy drain into a thermal result. That needs to be accounted for.

The trap that we both fell into was thinking for just a moment about a momentum accounting. No momentum is lost when the object and the air dissipate the energy of their relative motion into thermal energy. So we do not have to account for that momentum. But we are not accounting for momentum. We are accounting for energy. Those are the books that we need to balance.

We can do a momentum accounting easily enough if that is desired. It is quick and easy:

Over the course of one second, 3 kg of air is encountered and accelerated by 3 m/s. Total 9 kg m/s of momentum per second of travel. That's 9 N.

 

[axim]

The trap that we both fell into was thinking for just a moment about a momentum accounting. No momentum is lost when the object and the air dissipate the energy of their relative motion into thermal energy. So we do not have to account for that momentum. But we are not accounting for momentum. We are accounting for energy. Those are the books that we need to balance.

Hmmm. I gave it some more thoughts. I think I was accounting for it, as in the energy required for acceleration (6.75Nm) there are 2.25Nm which are dissipated in the next collision. And to me it still looks like there is a difference if this acceleration happens continuously or in intervals (slowing down, then accelerating again instead of a continuous movement).
Then I spent some time thinking about the impulse change, force over time. If I use the average force from your momentum accounting (9N supplied continuously), it means I end up in my continuous Case B.

Then I wondered, what does my case A (discontinuous) really mean. I can easily keep the average force of 9N over time the same, but vary the time when there is 0 force ("observing" the collision), and then double force (accelerating object and air again). This is basically what I calculated in the previous post in case A.
But, this would also mean as I have a deceleration and then an acceleration, the average speed would be reduced. So I would actually not be moving the object with 3m/s in average. I could then accelerate it to >3m/s for some time to compensate this, but then calculations and what I'm trying to model will really get out of hand.

 

[jbriggs444]

Hmmm. I gave it some more thoughts. I think I was accounting for it, as in the energy required for acceleration (6.75Nm) there are 2.25Nm which are dissipated in the next collision. And to me it still looks like there is a difference if this acceleration happens continuously or in intervals (slowing down, then accelerating again instead of a continuous movement).

I believe that you are correct. However, there is a way out of the conundrum that seems to result.

Let me try the mechanical energy accounting.

You have 1 kg of stationary air going into the interaction and 1 kg of moving air coming out.

The delta is $\frac{1}{2}(1) \times (3)^2$. That is a delta of 4.5 J

You have 1 kg of moving object going into the interaction and 1 kg of moving object coming out.

That is a delta of 0 J.

How much mechanical energy are we dissipating into frictional losses? You have a calculation that suggests that it is 2.25 J.

You envision an interaction where the object coasts, decellerating while a packet of air collides inelastically.

You then apply a force to both air and object, causing them to accelerate together. Under this model, we have a force that is not applied to object+air, not to object alone.

I must agree that in this scenario, the amount of energy delivererd to the system in the form of work totals 6.75 J over the course of the 1 meter interaction.

We also have an object that is not moving uniformly at 3 m/s. Its average velocity will depend on how rapidly it slows down for each interaction and on how rapidly we accelerate it back to 3 m/s after each interaction.

Suppose that we make the decelleration and the subsequent re-acceleration nearly instantaneous. Then we will retain our 3 m/s speed as an average. Then we face the apparent conundrum: 9 N of force (from the momentum argument) times 1 meter of distance. We've injected 9 J in and gotten only 6.75 J out.

There is a resolution to this conundrum. The force is not applied to an object that is moving at 3 m/s. It is applied to a pair of objects moving at a speed that ranges from 1.5 m/s to 3.0 m/s with an average of 2.25 m/s during the interval where the force is applied. The work done by that 9 N (average) force is 3 * 2.25 = 6.75 J.

6.75 J of energy out. 6.75 J of energy in.Now let us shift to the continuous motion model and do the energy accounting again.

You have 1 kg of stationary air going into the interaction and 1 kg of moving air coming out.

The delta is $\frac{1}{2}(1) \times (3)^2$. That is a delta of 4.5 J

You have 1 kg of moving object going into the interaction and 1 kg of moving object coming out.

That is a delta of 0 J.

How much mechanical energy are we dissipating into frictional losses? I have a calculation which you may find convincing. While a 1 kg packet of air is moving against the object and being accelerated from 0 m/s to 3 m/s, it slides some distance relative to the object. It will turn out not to matter how rapid or how slow the acceleration is. A gentle force will last a long time and involve a long slide. A strong force will last a short while and involve a short slide. The energy dissipated into heat will turn out to be the product (actually the integral of the product) of relative velocity and total momentum transferred.

1.5 m/s average relative velocity times 3 kg m/s momentum transferred means 4.5 J of thermal losses.

4.5 J of mechanical energy plus 4.5 J of thermal energy means 9 J of energy requirements.

This time the external force is pushing on the object alone. And the object is moving at a constant speed for the 1 meter traversed. A force of 9 N will do the trick.

9 J in, 9 J out.

 

[axim]

Suppose that we make the decelleration and the subsequent re-acceleration nearly instantaneous. Then we will retain our 3 m/s speed as an average. Then we face the apparent conundrum: 9 N of force (from the momentum argument) times 1 meter of distance. We've injected 9 J in and gotten only 6.75 J out.

Yes, that is really a conundrum which started my head spinning initially! Great point about the almost instantaneous acceleration/deceleration to make the thoughts easier here.

There is a resolution to this conundrum. The force is not applied to an object that is moving at 3 m/s. It is applied to a pair of objects moving at a speed that ranges from 1.5 m/s to 3.0 m/s with an average of 2.25 m/s during the interval where the force is applied. The work done by that 9 N (average) force is 3 * 2.25 = 6.75 J.

The average speed also took me time to realize and I stepped into a trap before... Makes perfect sense now.

1.5 m/s average relative velocity times 3 kg m/s momentum transferred means 4.5 J of thermal losses.

4.5 J of mechanical energy plus 4.5 J of thermal energy means 9 J of energy requirements.

Yes.
Now I could finally go back to my initial problem... With the knowledge we developed here I think I can draw some conclusions:
It does make a difference, if the changes happen continuously or sequential.
I did now also re-calculate my second reference frame, object moving at 2m/s with 1m/s headwind compared against our now studied example with the object moving at 3m/s and no headwind.
Calculating it with a sequential deceleration and acceleration, I get a different value for the required work: 5.625Nm instead of 6.75Nm for each meter of movement. I think it also makes sense as the relative movement is different: first deceleration to 0, then acceleration to +0.5m/s, and then a frictionless acceleration to 2m/s has a different "slippage" (average speed=1.25m/s while force is applied) than the acceleration from 0 to 1.5m/s and then frictionless to 3m/s (average speed 2.25m/s).

But, and that is my new insight, with a continuous movement I finally get the same results for the required work in both frames. Which I'm happy with because I never calculated it that way and I couldn't wrap my head around why I can just change the reference frame like this.
Footnote: I think the reference frame can be changed only with the continuous movement, which I guess is fine with fluid mechanics, but I need to be careful in other cases.