QuantumRose
- 11
- 1
The question:
Show that the Lorentz condition ∂µAµ =0 is expressed as d∗ A =0.
Where A is the four-potential and * is the Hodge star, d is the exterior differentiation.
In four-dimensional space, we know that the Hodge star of one-forms are the followings.

3. My attempt
Since the four potential one-form is

Therefore we have

Then d*A = 0 is equivalent of saying
 (Where
(Where
 )
)
However, the actual Lorentz gauge potential is
 (Where
(Where
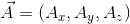 )
)
I don't know why there is a sign difference?
Show that the Lorentz condition ∂µAµ =0 is expressed as d∗ A =0.
Where A is the four-potential and * is the Hodge star, d is the exterior differentiation.
In four-dimensional space, we know that the Hodge star of one-forms are the followings.

3. My attempt
Since the four potential one-form is
Therefore we have
Then d*A = 0 is equivalent of saying
However, the actual Lorentz gauge potential is
I don't know why there is a sign difference?