Acceleration for a non-inertial reference frame

[Like Tony Stark]

Homework Statement

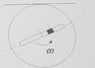
The disk with a slot rotates with $\omega =20 \frac{rad}{s}$ about a vertical axis that passes through its centre. There's a slider of mass $0.73 kg$ that oscilates because of the action of a spring (not shown in the picture) and it has a positive velocity $90 \frac{cm}{s}$ relative to the disk when it is in $x=0$. Determine the normal force exerted by the slot on the slider when $x=0$.

Relevant Equations

$a_I=a_o+\dot \omega \times r+\omega \times (\omega \times r)+2(\omega \times v_{rel}) +a_{rel}$.

Well, first a wrote the equation for acceleration in non inertial systems.

$a_I=a_o+\dot \omega \times r+\omega \times (\omega \times r)+2(\omega \times v_{rel}) +a_{rel}$.

Then, $a_o=0$ (because the system doesn't move), $a_i=0$ (because it is measured from the non inertial system), $\dot \omega =0$ (because the angular velocity is constant), $r=0$ (because $x=0$)

So we get
$-2 (\omega \times v_{rel})=a_{rel}$

Then, we write Newton's equations
$x) Fe=m.a_{rel}$
$y) N-F_{Cor}=0$

Where $Fe$ is the elastic force and $F_{Cor}=2(\vec \omega \times v_{rel})$

So I just have to replace with the numbers that I was given and get $N$.

Are my ideas correct?

 

[kuruman]

There are two non-inertial frames, one fixed on the platform and one fixed on the slider. Which one are you considering? When you say that $a_0=0$ because the "system doesn't move" which system is this? What are you going to use for $v_{rel}$? Also, don't replace any numbers before you get an expression for $N$ in terms of symbols all of which are given. That will make it easier to check your work.

 

[Like Tony Stark]

There are two non-inertial frames, one fixed on the platform and one fixed on the slider. Which one are you considering? When you say that $a_0=0$ because the "system doesn't move" which system is this? What are you going to use for $v_{rel}$? Also, don't replace any numbers before you get an expression for $N$ in terms of symbols all of which are given. That will make it easier to check your work.

I'm considering a system fixed to the platform. I said that $a_0=0$ because the origin doesn't move. Then I said that $a_i$ is the acceleration measured from an inertial frame, but as I took the disk frame, I said that it was 0.

As for not replacing the numbers, yes, I'll take your advice, but I replaced them to check if the data that I plugged in was ok.

 

[kuruman]

So what's your symbolic answer?

 

[Like Tony Stark]

So what's your symbolic answer?

$y)N-\Sigma F_{rely}=m.a_{rely}$
$N=\Sigma F_{rely}+m.a_{rely}$

Where $\Sigma F_{rely}$ is the sum of the pseudo-forces acting on the $y$ direction and $a_{rely}$ is the acceleration of the slider relative to the disk.

 

[kuruman]

$y)N-\Sigma F_{rely}=m.a_{rely}$
$N=\Sigma F_{rely}+m.a_{rely}$

Where $\Sigma F_{rely}$ is the sum of the pseudo-forces acting on the $y$ direction and $a_{rely}$ is the acceleration of the slider relative to the disk.

Not what I had in mind. I am asking for an expression giving $N$ in terms of symbols for which you have numbers. You don't have numbers for any of the quantities on the right hand side except for the mass $m$.

 

[Like Tony Stark]

Not what I had in mind. I am asking for an expression giving $N$ in terms of symbols for which you have numbers. You don't have numbers for any of the quantities on the right hand side except for the mass $m$.

$y)N=m.a_{rely} -2(\omega \times v_{rel})$

$m$, $\omega$ and $v_{rel}$ are a given values; $a_{rely}=0$ because the slider just moves in $x$

 

[kuruman]

Almost correct. You need to multiply the second term by the mass. Also, the problem gives only magnitude of $\omega$, but I think it is safe to assume that it is in the $+z$ direction.