- #1
Like Tony Stark
- 179
- 6
- Homework Statement
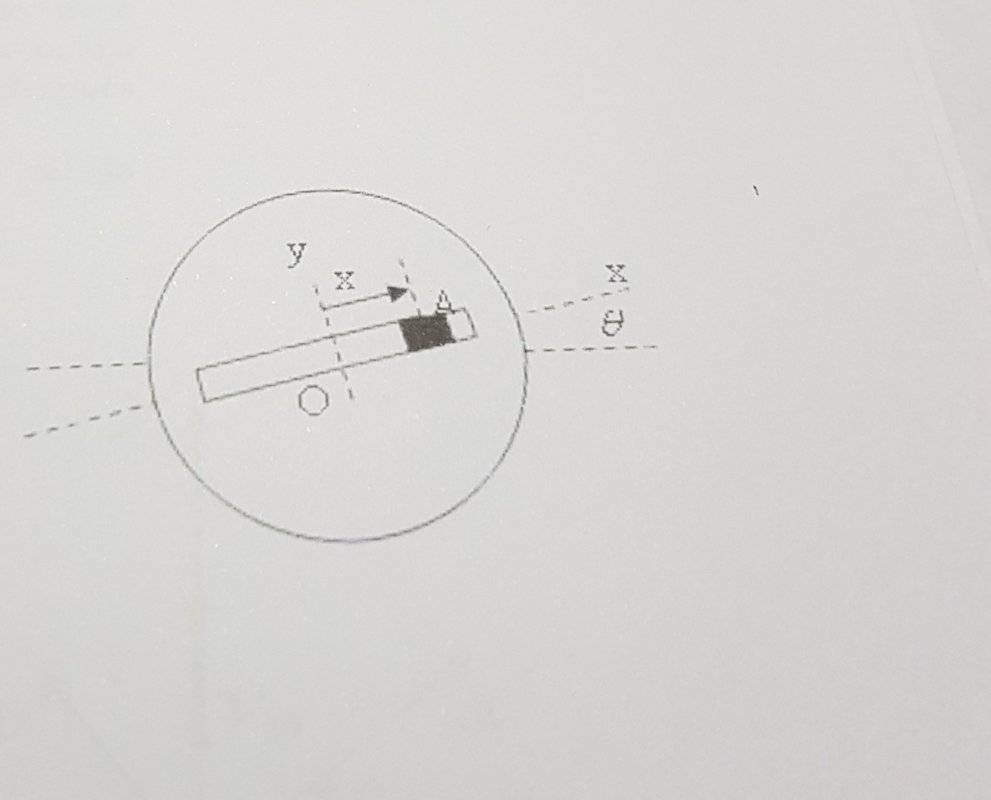
- ##A## oscillates along the central position ##O## with amplitude ##5 cm## at a frecuency ##2 hz## such that its displacement measured in ##cm## in function of time is governed by ##x=5sin(4 \pi t)##, where ##t## is measured in seconds. An angular acceleration around ##O## is applied to the disc with an amplitude ##20 rad## at a frequency ##4 hz## such that ##\theta =0.20sin(8 \pi t)##. Determine the acceleration of A for ##x=0 cm## and ##x= 5 cm##.
- Relevant Equations
- ##\vec a=\vec a_B + \vec{\dot \omega} X \vec r + \vec \omega X \vec \omega X \vec r + 2. \vec \omega . \vec v_{rel} + \vec a_{rel}##
The first doubt that comes to my mind is "I have to determine the acceleration with respect to what?", because the problem doesn't tell. Then, I have some problems when having to plug the data in the formula of acceleration. ##\vec a_B=0## because the origin isn't accelerated, ##\vec{\dot \omega} X \vec r## would be ##x=5sin(4 \pi .5)## (in the second case), and then what numbers should I plug in ##\vec \omega X \vec \omega X \vec r##, ##2. \vec \omega . \vec v_{rel}## and ##\vec a_{rel}##?
I don't understand relative rotational motion very well. I mean, I just have to plug the data in the formula, but I don't know what's the data that I have.
I don't understand relative rotational motion very well. I mean, I just have to plug the data in the formula, but I don't know what's the data that I have.