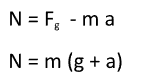Acceleration in Newton's second law

[ksy]

TL;DR Summary

In Newton's second law problems, some textbooks (like Halliday and Resnick) substitute "a" for a component of the acceleration, irrespective of its sign. Why is that possible?

Hi,

I was looking over one of the sample examples in Halliday and Resnick, the one
about the scale in the elevator. There is something that bugs me about it, and I'd
like to know if you agree.

The example has to do with finding the reading of a scale that is measuring
someone's weight in a moving, and especially accelerating elevator (where
the acceleration is measured in the ground frame to use Newton's 2nd law).
This reading is the same as the absolute value of the normal force from the person on the scale, and
therefore the absolute value of the normal force from the scale on the person,
from Newton’s third law.

The positive y direction is chosen to be upwards, as usual.

Newton's second law is then taken to be:

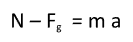
Surely that’s the equation for the y components of the vectors involved:

But at this stage, we don’t know the direction of the acceleration, so why are we
implicitly stating that

?
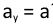Then, substituting mg for

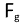that leads to:

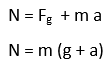
And so far, nothing has been said about whether the elevator is accelerating up or
down. So we don’t know whether the y component of a is positive or negative.

Now the example goes on to say that for the elevator accelerating up at 3.20 m/s^2 ,
a = + 3.20 m/s^2 so:
N = (72.2kg) (9.8 m/s^2 + 3.20 m/s^2 )

While if the elevator accelerates down at 3.20 m/s^2 ,
a = - 3.20 m/s^2 so:
N = (72.2kg) (9.8 m/s^2 - 3.20 m/s^2 )

To me, this only makes sense if

that is a component of a. Because
components can be positive or negative, while magnitudes are always positive.
And obviously at this point we are dealing with an algebraic equation, not a vector
one so we can’t mean a as a vector.
I’ve seen this done since I was in high school, when we were told “if you assume
the wrong direction for a, it will just come out negative”. I’ve seen it taught that
way in colleges and universities. And I’ve done it hundreds of times out of habit.
But now that I think about it, I can’t help wonder: how can assuming that

how can that not violate some kind of homogeneity and still be correct? What is "a"
in there?
If we want to get rid of the y subscript on "a" without first knowing in which
direction a points, surely we should write:

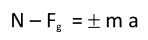
No??? Or what am I missing?

Thank you for your thoughts!!!

 

[Ibix]

Whether you choose to be explicit about it or not, you are using vectors when you add forces. So yes, they're adding components there. The general case is $\vec N+\vec W=m\vec a$, where I'm using $\vec W$ for the weight force, and in this 1d example there is one non-trivial component sum, $N_y+W_y=ma_y$. And we can plug in that $W_y=-mg$ where $g$ is defined to be a positive constant.

You are right that they probably shouldn't drop the $y$ subscript on the $a$, but do note that the same is true of $N$: in a lift accelerating downward at more than 1g you would be pinned to the ceiling and $\vec N$ would point in the -y direction. So both $N$ and $a$ in the equation you quote are formally $y$ components of their respective vectors. In this 1d case you can get away with notating them as some kind of signed magnitude, but it's arguably not particularly good practice. It certainly doesn't generalise to two or more dimensions.

 

[PeroK]

If we have a problem where motion in a single direction is considered, then there is nothing wrong with using the one dimensional real numbers for forces and displacements. Technically, the real numbers form a one dimensional vector space. And, in any case, real numbers can be positive and negative.

There's nothing wrong with ignoring the two other spatial dimensions if you don't need them.

In Newton's second law in one dimensional form $F = ma$, $a$ and $F$ are one dimensional vectors. Whereas, mass is a scalar.

 

[Chestermiller]

If you include the unit vectors in your equation, you can't go wrong.

 

[ksy]

they probably shouldn't drop the $y$ subscript on the $a$, but do note that the same is true of $N$: in a lift accelerating downward at more than 1g you would be pinned to the ceiling and $\vec N$ would point in the -y direction. So both $N$ and $a$ in the equation you quote are formally $y$ components of their respective vectors.

I hadn't thought about the case of a>g! Yes then N would point in the -y direction all right lol! Then again it would be N from the ceiling rather than the scale.

Ibik, PeroK, Chestermiller, thank you all very much for your help!