Homework Help Overview
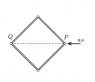
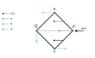
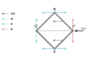
The problem involves a square frame made of four rods connected by frictionless hinges, with a force applied to one vertex, causing it to accelerate. The question seeks to determine the acceleration of the opposite vertex as a result of this force.
Discussion Character
- Exploratory, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants express difficulty in visualizing the movement of the frame when only one vertex is accelerated. There are discussions about drawing free body diagrams and identifying forces acting on the rods.
- Some participants suggest using symmetry to parameterize the movement and question how forces are distributed among the rods.
- Questions arise regarding the presence of vertical forces at certain junctions and the need for clarification on how to approach the problem mathematically.
Discussion Status
The discussion is ongoing, with participants exploring various interpretations of the forces involved and the dynamics of the system. Some have proposed drawing diagrams and writing equations, while others are seeking confirmation of their understanding of the forces acting on the rods.
Contextual Notes
Participants note the complexity of the problem due to the interactions between the rods and the need to consider both linear and angular accelerations. There is mention of constraints related to the assumptions made about the system's behavior.