- #1
peripatein
- 880
- 0
Hi,
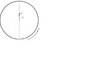
I am trying to determine the magnitude of the acceleration, registered by an observer in the lab, of mass m forced to move along a radial track, immediately as it begins moving along the track. Please see attachment. ω=αt and the entire set up is horizontal. The initial position of the mass is marked as r0 and it is stated that only static friction is present along the track, with coefficient μ, whereas kinetic friction is null.
As there is no friction once the mass begins moving, there are no forces in action (coriolis will not have an effect as the mass couldn't move in any direction but the radial). Hence, its acceleration, as registered by an observer in the lab, will be zero. Is this correct?
Homework Statement
I am trying to determine the magnitude of the acceleration, registered by an observer in the lab, of mass m forced to move along a radial track, immediately as it begins moving along the track. Please see attachment. ω=αt and the entire set up is horizontal. The initial position of the mass is marked as r0 and it is stated that only static friction is present along the track, with coefficient μ, whereas kinetic friction is null.
Homework Equations
The Attempt at a Solution
As there is no friction once the mass begins moving, there are no forces in action (coriolis will not have an effect as the mass couldn't move in any direction but the radial). Hence, its acceleration, as registered by an observer in the lab, will be zero. Is this correct?