Cato11
- 46
- 11
I would really appreciate some help with a challenge I have. It is illustrated in the figure below:
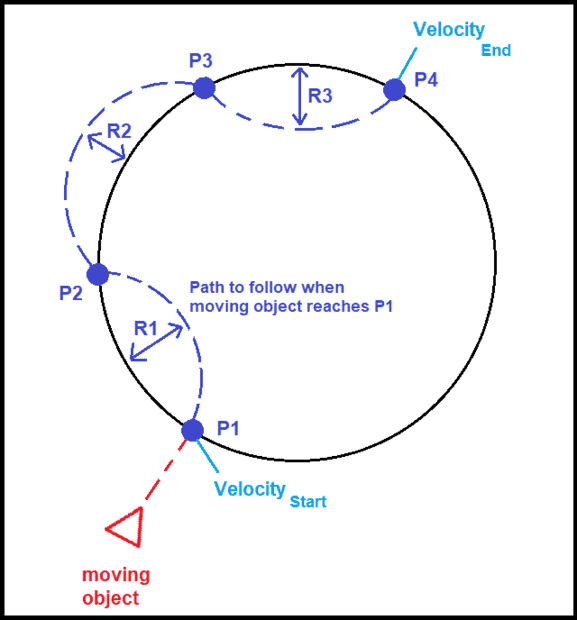
Scenario: The moving object moves with linear velocity until it reaches P1. When it reaches P1, I need to create the motion of the blue dashed path. Whilst the object follows the blue dashed path, it needs to uniformly accelerate from Velocity(start) to Velocity(end).
The following pieces of information are known:
What I have already tried:
Note: The figure is merely a sketch and thus the curving of the arcs is a rough approximation. In reality, the arcs should connect with a more natural curvature, without the abrubt changes in direction.
Scenario: The moving object moves with linear velocity until it reaches P1. When it reaches P1, I need to create the motion of the blue dashed path. Whilst the object follows the blue dashed path, it needs to uniformly accelerate from Velocity(start) to Velocity(end).
The following pieces of information are known:
- Velocity (start), e.g. 5 m/s
- Velocity (end), e.g. 10 m/s
- The locations of the four points P1 - P4
- The location of the centre of the circle
What I have already tried:
- Separating the path into three separate arcs using bezier curves. This has been partially successful - I can approximate the path but with constant speed. I do not understand how to achieve acceleration through the curves. Also, the bezier method uses additional control points to approximate the arcs; it would be better if I could define the R1-3 values and somehow achieve precisely that motion, but I do not know how to do this.
Note: The figure is merely a sketch and thus the curving of the arcs is a rough approximation. In reality, the arcs should connect with a more natural curvature, without the abrubt changes in direction.
Last edited: