- 893
- 483
- TL;DR
- Conventional wisdom says that when a subsonic gas flow accelerates through a converging duct, it can only achieve Mach 1 at the point of minimal area (throat). The math makes sense but I don't understand the physics that makes this happen on the local scale. I also have incomplete simulation results that I don't understand.
For compressible flow in a duct, mass conservation combined with reversibility (no entropy change) implies $$(1-\frac{u^2}{c^2})\frac{du}{u} = -\frac{dA}{A}$$
where u is the flow velocity of the gas, c is the speed of sound in the gas, and A is the area of the duct. I am assuming a calorically perfect, ideal gas (ideal gas law holds for u = 0 and constant heat capacities, but ##γ=\frac{c_p}{c_v}## need not be 5/3, as it would be for a true ideal gas with no internal structure). Based on these assumptions, the speed of sound is ##c=\sqrt{γRT}## where R is the specific gas constant (universal gas constant divided by molar mass, ## R = \frac{\bar{R}}{M}##). Just to be extra clear, this flow is adiabatic, not isothermal, so the speed of sound is not constant.
Now, the argument I see in the textbooks is that when a flow gets accelerated to Mach 1, the left hand side of the above equation goes to zero, therefore ##dA=0##. The textbooks interpret this to mean that Mach 1 only ever occurs at the throat. I understand the argument on mathematical grounds. Originally, my physical intuition was that as the gas flows it compresses, and so the temperature rises. As the temperature rises, the speed of sound increases. As a result, the flow can only approach Mach 1 asymptotically, with the speed of sound and flow velocity increasing at almost equal rates. However, this does not agree with my numerical results.
In my simulations, I see the flow velocity approach Mach 1 sharply, followed by pathological behavior of the numerics once Mach 1 is reached. Extrapolating the non-pathological regime suggests that the flow really does reach Mach 1.
I have also done this simulation with a fixed step solver I wrote in C++, but the code is not easy to read and it calls several external tools, so it'd be a real hassle for anyone to either try to deciper it or try to run it on their own system. I'll just say that the qualitative results are identical, namely that the Mach number approaches 1 sharply.
[CODE lang="matlab" title="Octave/Matlab Version (simple):"]
R = 8.314 / (44.01E-3); %specific gas constant for propane
g = 1.13; %heat capacity ratio
r1 = 0.5 / 2 * 2.54e-2; %initial radius in meters (0.5 inches)
r2 = 0.031 / 2 * 2.54e-2; %final radius in meters (0.031 inches)
A1 = pi*r1^2;
A2 = pi*r2^2;
p1 = (30 + 14.7)/14.7 * 101500; %initial pressure in bar (30psi gauge at inlet)
T1 = (40 -32) * (5/9) + 273; %initial temperature in Kelvin (40 Fahrenheit)
u1 = 10; %initial flow velocity in m/s
T0 = (R*T1 + 0.5 * (1-1/g)*u1^2)/R; %stagnation temperature, from Bernoulli equation & ideal gas law
p0 = (T0/T1)^(g/(g-1)) * p1; %stagnation pressure, from adiabatic flow relations
rho0 = p0/R/T0; %stagnation density, from ideal gas law
rho1 = (T1/T0)^(1/(g-1)) * rho0; %initial density, from adiabatic flow relations
c0 = sqrt(g*R*T0); %speed of sound at stagnation point
dudA = @(A,u) - (real(u)/A) / (1 - (real(u)/c0)^2 * (rho0*real(u)*A/u1/A1/rho1)^(g-1));
meh = ode45(dudA,[A1,A2],u1);
% note: the use of "real" is just to force MATLAB to only consider the real part
u = meh.y; A = meh.x;
rho = (((A1*u1) ./ A) ./ real(u)) * rho1; %local density, from mass conservation
p = rho .* (p0/rho0 - 0.5 * (1- 1/g) * real(u).^2); %local pressure, from Bernoulli equation
T = (rho/rh .^(g-1) * T0; %local temperature from adiabatic flow relations
.^(g-1) * T0; %local temperature from adiabatic flow relations
c = sqrt(g*R*T); %local speed of sound
%figure(1); clf;
%plot(A,real(u)./c)
%xlabel('Duct Area (m^2)')
%ylabel('Local Mach Number')
% Sanity check: local entropy
% Get the stagnation states for each local thermodynamic state
l_T0 = (R*T + 0.5*(1-1/g)*real(u).^2)/R;
l_p0 = (l_T0./T).^(g/(g-1)) .* p;
for n = 1:length(u)
s(n) = CoolProp.PropsSI("S","T",double(l_T0(n)),"P",double(l_p0(n)),"Propane"); %lookup mass specific entropy
end
figure(1); clf;
subplot(2,1,1)
plot(A,real(u)./c)
xlabel('Duct Area (m^2)')
ylabel('Local Mach Number')
subplot(2,1,2)
plot(A,s/1000)
xlabel('Duct Area (m^2)')
ylabel('Specific entropy (kJ/(kg*K))')
[/CODE]
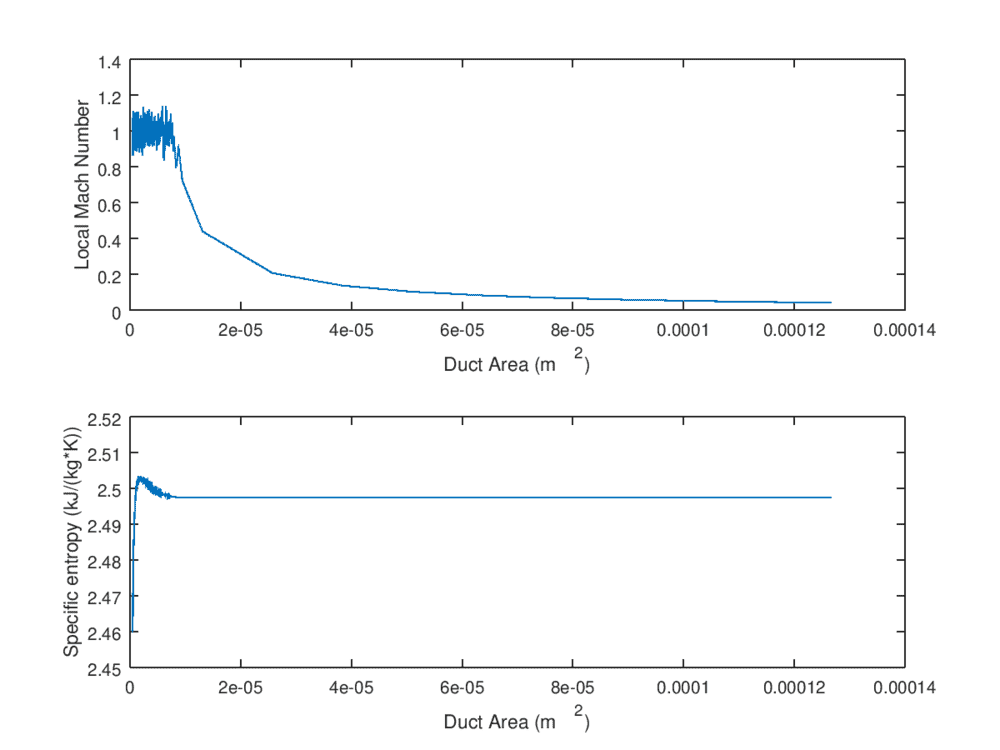
I put the entropy in there so you know where to stop trusting the numerics.
where u is the flow velocity of the gas, c is the speed of sound in the gas, and A is the area of the duct. I am assuming a calorically perfect, ideal gas (ideal gas law holds for u = 0 and constant heat capacities, but ##γ=\frac{c_p}{c_v}## need not be 5/3, as it would be for a true ideal gas with no internal structure). Based on these assumptions, the speed of sound is ##c=\sqrt{γRT}## where R is the specific gas constant (universal gas constant divided by molar mass, ## R = \frac{\bar{R}}{M}##). Just to be extra clear, this flow is adiabatic, not isothermal, so the speed of sound is not constant.
Now, the argument I see in the textbooks is that when a flow gets accelerated to Mach 1, the left hand side of the above equation goes to zero, therefore ##dA=0##. The textbooks interpret this to mean that Mach 1 only ever occurs at the throat. I understand the argument on mathematical grounds. Originally, my physical intuition was that as the gas flows it compresses, and so the temperature rises. As the temperature rises, the speed of sound increases. As a result, the flow can only approach Mach 1 asymptotically, with the speed of sound and flow velocity increasing at almost equal rates. However, this does not agree with my numerical results.
In my simulations, I see the flow velocity approach Mach 1 sharply, followed by pathological behavior of the numerics once Mach 1 is reached. Extrapolating the non-pathological regime suggests that the flow really does reach Mach 1.
I have also done this simulation with a fixed step solver I wrote in C++, but the code is not easy to read and it calls several external tools, so it'd be a real hassle for anyone to either try to deciper it or try to run it on their own system. I'll just say that the qualitative results are identical, namely that the Mach number approaches 1 sharply.
[CODE lang="matlab" title="Octave/Matlab Version (simple):"]
R = 8.314 / (44.01E-3); %specific gas constant for propane
g = 1.13; %heat capacity ratio
r1 = 0.5 / 2 * 2.54e-2; %initial radius in meters (0.5 inches)
r2 = 0.031 / 2 * 2.54e-2; %final radius in meters (0.031 inches)
A1 = pi*r1^2;
A2 = pi*r2^2;
p1 = (30 + 14.7)/14.7 * 101500; %initial pressure in bar (30psi gauge at inlet)
T1 = (40 -32) * (5/9) + 273; %initial temperature in Kelvin (40 Fahrenheit)
u1 = 10; %initial flow velocity in m/s
T0 = (R*T1 + 0.5 * (1-1/g)*u1^2)/R; %stagnation temperature, from Bernoulli equation & ideal gas law
p0 = (T0/T1)^(g/(g-1)) * p1; %stagnation pressure, from adiabatic flow relations
rho0 = p0/R/T0; %stagnation density, from ideal gas law
rho1 = (T1/T0)^(1/(g-1)) * rho0; %initial density, from adiabatic flow relations
c0 = sqrt(g*R*T0); %speed of sound at stagnation point
dudA = @(A,u) - (real(u)/A) / (1 - (real(u)/c0)^2 * (rho0*real(u)*A/u1/A1/rho1)^(g-1));
meh = ode45(dudA,[A1,A2],u1);
% note: the use of "real" is just to force MATLAB to only consider the real part
u = meh.y; A = meh.x;
rho = (((A1*u1) ./ A) ./ real(u)) * rho1; %local density, from mass conservation
p = rho .* (p0/rho0 - 0.5 * (1- 1/g) * real(u).^2); %local pressure, from Bernoulli equation
T = (rho/rh
 .^(g-1) * T0; %local temperature from adiabatic flow relations
.^(g-1) * T0; %local temperature from adiabatic flow relationsc = sqrt(g*R*T); %local speed of sound
%figure(1); clf;
%plot(A,real(u)./c)
%xlabel('Duct Area (m^2)')
%ylabel('Local Mach Number')
% Sanity check: local entropy
% Get the stagnation states for each local thermodynamic state
l_T0 = (R*T + 0.5*(1-1/g)*real(u).^2)/R;
l_p0 = (l_T0./T).^(g/(g-1)) .* p;
for n = 1:length(u)
s(n) = CoolProp.PropsSI("S","T",double(l_T0(n)),"P",double(l_p0(n)),"Propane"); %lookup mass specific entropy
end
figure(1); clf;
subplot(2,1,1)
plot(A,real(u)./c)
xlabel('Duct Area (m^2)')
ylabel('Local Mach Number')
subplot(2,1,2)
plot(A,s/1000)
xlabel('Duct Area (m^2)')
ylabel('Specific entropy (kJ/(kg*K))')
[/CODE]
I put the entropy in there so you know where to stop trusting the numerics.