Discussion Overview
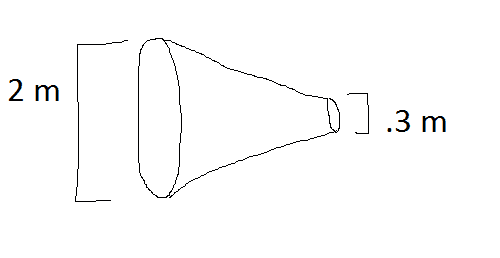
The discussion revolves around calculating the velocity of air flowing through a tapered tube, starting from a wider opening. Participants explore the appropriate equations to use for both incompressible and compressible flow scenarios, considering the implications of flow speed and area changes.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- Some participants propose using the equation Q = v * A to calculate flow, questioning its applicability to the scenario presented.
- Others argue that the equation is valid only for incompressible flow and may not yield accurate results for compressible fluids.
- A participant mentions that gases can be assumed incompressible at flow speeds below a certain threshold, specifically under 100-120 m/s for air.
- One participant suggests that compressible flow might result in higher speeds under certain idealized conditions, while acknowledging real-world factors like friction that could affect flow rates.
- Another participant points out that once flow speed reaches the speed of sound, further increases in speed are constrained, and any mass flow rate increase would involve changes in pressure and density.
- A participant identifies a potential error in the original calculations regarding the outlet velocity, suggesting that the correct approach involves compressible flow equations, leading to a different outlet velocity than initially calculated.
- There is a discussion about the complexity of equations for compressible flow and the challenges of conveying this information effectively to those unfamiliar with the topic.
Areas of Agreement / Disagreement
Participants express differing views on the applicability of the incompressible flow equation and the implications of compressibility on flow speed. There is no consensus on a single correct approach, and the discussion remains unresolved regarding the best method to calculate the outlet velocity.
Contextual Notes
Participants note that the analysis may depend on specific assumptions about flow conditions, such as speed and compressibility, and that the original calculations may have overlooked certain factors like the correct conversion of dimensions.