Ampere's Law and Conductor: Finding ∫B.dl for a Semicircle in the x-z Plane

[Tanya Sharma]

Homework Statement

A conductor carrying current ‘I’ is in the form of a semicircle AB of radius ‘R’ and lying in the x-y plane with its centre at origin as shown in the figure. Find the magnitude of ∫B.dl for the circle 3x² +3z² =R² in the x-z plane due to curve AB.

Ans (1-√3/2)μ₀I

Homework Equations

The Attempt at a Solution

Applying Ampere’s Law ∫B.dl= μ₀I for the closed loop i.e the given circle ∫B.dl turns out to be zero since there is no current flowing through the loop .But this is incorrect .

I would be grateful if somebody could help me with the problem.

 

[TSny]

Hello, Tanya.

Ampere's law only applies to a current that is part of a complete circuit. The current can't just start at A and end at B. So, you'll have to imagine a way to complete the circuit if you want to use Ampere's law.

(Do you have a typographical error in your equation for the circular path in the x-z plane?)

 

[Tanya Sharma]

Hi TSny

Thanks for the response .

Yes ,there was a typo in the equation for circular path . I have fixed it .

Should I join the path from B to A to complete the circuit ?

 

[TSny]

Hi TSny

Thanks for the response .

Yes ,there was a typo in the equation for circular path . I have fixed it .

Should I join the path from B to A to complete the circuit ?

Maybe.

 

[nrqed]

Hi TSny

Thanks for the response .

Yes ,there was a typo in the equation for circular path . I have fixed it .

Should I join the path from B to A to complete the circuit ?

I think you are expected to ignore any wire beside the one shown because you may take for granted that anything else will not produce any flux through your surface (for example, the remaining wire could extend away along the y axis). Just obtain the magnetic field produced by the section shown and calculate the line integral (or calculate the integral of \int \vec{B} \cdot \vec{dA} and use Stokes theorem if you have seen that).

 

[Tanya Sharma]

Maybe.

I am actually smiling while reading this .

This gives correct answer .

So basically the semicircular conductor carrying current is equivalent to a closed circuit conducting path from A to B ( semi circle ) and B to A ( straight line ) .

Does that sound right ?

 

[TSny]

So basically the semicircular conductor carrying current is equivalent to a closed circuit conducting path from A to B ( semi circle ) and B to A ( straight line ) .

Does that sound right ?

Well, the semicircular current alone is not equivalent to a closed current loop which consists of the semicircular part plus a straight current from B to A. Perhaps I'm misinterpreting what you are saying.

You want to find ∫Bdl for the field of just the semicircle current. This is not the same as ∫Bdl for the complete closed loop consisting of the semicircle and straight line. But you can relate the two ∫Bdl 's using ideas of superposition.

 

[rude man]

I am actually smiling while reading this .

This gives correct answer .

So basically the semicircular conductor carrying current is equivalent to a closed circuit conducting path from A to B ( semi circle ) and B to A ( straight line ) .

Does that sound right ?

I don't see the rationale in doing that. (Which means nothing, really.)

Personally I would have used Biot-Savart to find B(x,z), then integrated B.ds.

 

[TSny]

I don't see the rationale in doing that. (Which means nothing, really.)

Personally I would have used Biot-Savart to find B(x,z), then integrated B.ds.

Hi, rude man. You can use Biot-Savart for the semicircular current, but it looks a little messy to me. I think it's easier to use Ampere's law and some judicious superpostion so that you only have to use Biot-Savart for a simpler geometrical current distribution.

 

[Tanya Sharma]

Well, the semicircular current alone is not equivalent to a closed current loop which consists of the semicircular part plus a straight current from B to A. Perhaps I'm misinterpreting what you are saying.

You want to find ∫Bdl for the field of just the semicircle current. This is not the same as ∫Bdl for the complete closed loop consisting of the semicircle and straight line. But you can relate the two ∫Bdl 's using ideas of superposition.

Ok

Magnetic field due to straight wire BA at the circular path $B' = \frac{3μ_0I}{4\pi R}$

Magnetic field due to semi circular wire AB = $B$

$\oint \vec{B'} \cdot \vec{dl} = \frac{\sqrt{3}μ_0I}{2}$

$\oint \vec{B} \cdot \vec{dl} + \oint \vec{B'} \cdot \vec{dl} = μ_0I$

$\oint \vec{B} \cdot \vec{dl} = μ_0I(1-\frac{\sqrt{3}}{2})$

Why is it giving correct answer ? I may have made some calculation mistake .

 

[TSny]

Ok

Magnetic field due to straight wire BA at the circular path $B' = \frac{3μ_0I}{4\pi R}$

Magnetic field due to semi circular wire AB = $B$

$\oint \vec{B'} \cdot \vec{dl} = \frac{\sqrt{3}I}{2}$

$\oint \vec{B} \cdot \vec{dl} + \oint \vec{B'} \cdot \vec{dl} = μ_0I$

$\oint \vec{B} \cdot \vec{dl} = μ_0I(1-\frac{\sqrt{3}}{2})$

That looks good.

Why is it giving correct answer ? I may have made some calculation mistake .

Not sure why you have some doubt. Looks like you are using the idea of superposition as illustrated in the attached picture. You do want to make sure you understand the signs of the various terms (which depend on which way the currents are flowing and which way you are integrating around the circular path).

 

[rude man]

I will stipulate B' = 3μ₀I/4πR as derived by Biot-Savart. (I didn't check it but OK).

But then why not ∫B' dl = 3μ₀I/4πR * √3(2πR) = 3√3μ₀I/2 ?

And then how can ampere be used with the completed semicircle plus straight wire? How can that closed semicircle circuit be interpreted by ∫B.dl = μ₀I?

 

[TSny]

I will stipulate B' = 3μ₀I/4πR as derived by Biot-Savart. (I didn't check it but OK).

But then why not ∫B' dl = 3μ₀I/4πR * √3(2πR) = 3√3μ₀I/2 ?

What is the radius of the circular path of integration (3x² + 3z² = R²)?

And then how can ampere be used with the completed semicircle plus straight wire? How can that closed semicircle circuit be interpreted by ∫B.dl = μ₀I?

Not sure I'm following. Ampere's law can be used for any distribution of steady current and any shape of path of integration. For the completed semicircular current loop, Ampere's law will hold when integrating over the circular path in the x-z plane. The value of B in Ampere's law is the net magnetic field (at a point on the path of integration) due to all current elements in the complete circuit of current.

 

[rude man]

What is the radius of the circular path of integration (3x² + 3z² = R²)?

sqrt(3)

Not sure I'm following. Ampere's law can be used for any distribution of steady current and any shape of path of integration. For the completed semicircular current loop, Ampere's law will hold when integrating over the circular path in the x-z plane. The value of B in Ampere's law is the net magnetic field (at a point on the path of integration) due to all current elements in the complete circuit of current.

The net current due to the complete semicircular wire piercing the x-z circle = 0!

 

[TSny]

To get the radius of the circular path, write the equation as x² + z² = R²/3.

The attached picture shows the "completed" path of current (to form a complete circuit). There's a current going through the path of integration. The magnetic field in Ampere's law at points on the path of integration is the net field due to the semicircle and the straight section.

 

[rude man]

Oops, I got the radius wrong. It's 1/sqrt(3). Senior moment .. thanks for your patience!

 

[Tanya Sharma]

Not sure why you have some doubt. Looks like you are using the idea of superposition as illustrated in the attached picture. You do want to make sure you understand the signs of the various terms (which depend on which way the currents are flowing and which way you are integrating around the circular path).

I may have used the idea of superposition but this is not what I intended in post#10 :shy:. I didn't take straight conductor AB into consideration or did I ?

I thought of the semicircular conductor as equivalent to the closed loop .This means I am still not sure with Ampere's Law and superposition principle.

Are we applying Ampere's law to only closed loop ? Then what is the role of straight conductor AB (in which current is flowing in opposite direction) ?How are we integrating the two concepts i.e how are we using the superposition principle ? Could you reflect more on the sign issue ?

 

[TSny]

Does this picture help?

 

[Tanya Sharma]

I may be having trouble with signs .

Suppose we consider direction of current I to be positive downwards with B' positive clockwise .

Then while using Biot Savart Law to calculate ∫B'.dl , I would use $\oint- \vec{B'} \cdot \vec{dl} = -\frac{\sqrt{3}μ_0I}{2}$ ,as B' and I for red current would be in opposite directions to that of blue current .

The minus sign on both the sides cancel and we are left with $\oint \vec{B'} \cdot \vec{dl} = \frac{\sqrt{3}μ_0I}{2}$

We then use this result while applying Ampere's law to the loop .

Is it correct ?

 

[TSny]

I may be having trouble with signs .

Suppose we consider direction of current I to be positive downwards with B' positive clockwise .

Then while using Biot Savart Law to calculate ∫B'.dl , I would use $\oint- \vec{B'} \cdot \vec{dl} = -\frac{\sqrt{3}μ_0I}{2}$ ,as B' and I for red current would be in opposite directions to that of blue current .

The minus sign on both the sides cancel and we are left with $\oint \vec{B'} \cdot \vec{dl} = \frac{\sqrt{3}μ_0I}{2}$

We then use this result while applying Ampere's law to the loop .

Is it correct ?

You use Biot-Savart to find the magnitude and direction of B' on the path of integration due to the red current alone. You find that the direction of B' is counterclockwise as viewed from above.

Then $\small \oint \vec{B\:'} \cdot \vec{dl}$ $\small = \pm |B \: '|\; 2\pi R / \sqrt{3}$, where the sign will depend on whether you choose to integrate counterclockwise or clockwise around the path.

You then combine this result with the result for $\small \oint \vec{B \:''} \cdot \vec{dl}$ for the D-shaped loop (containing the blue current) which is easily found from Ampere's law. Of course you should integrate around the path in the same direction you chose for the red current. Here I have used the notation B'' for the field produced by the D-loop. (The field produced by just the black semicircular current alone is the vector sum of B' and B''.)

 

[rude man]

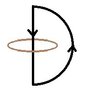
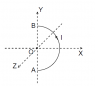Here's what I find interesting: the fact that for the straight wire alone, Biot-Savart must be used, while for the SAME straight wire as part of a complete circuit ampere's law can be used.

This aspect of Ampere's law is I believe not generally well taught. Typically, texts speak of a "long wire", often without even explaining why the wire should be long. Then, in a case like this where the wire is NOT long, folks can understandably be made nervous as to whether ampere can really be applied.

Take the case of a square of wire, side 2R, carrying current I. A perfectly realizable circuit. Now we (fallaciously) isolate one side of the square and apply ampere's law to a circular path, radius R, the circle's center at the center of the side, letting the current in the other 3 sides = 0. This computes to a uniform H field = I/2πR including at the square's center. Now we do the same for the other 3 sides, one at a time, each also giving H = I/2πR. Then we argue superposition and compute the H field at the center of the square = 2I/πR. Wrong answer! Ampere's law is inapplicable because each isolated segment of wire is not part of a complete circuit, so no realizable current could pass thru a closed contour as all the textbooks show, and even though the four segments together do form a closed circuit.

(On the other hand, ∫H.dl = I is correct for any segment providing all the other segments are also carrying I, in which case the symmetry of H around each loop is totally distorted, making computing H at the square's center impossible. )

I have seen several posters get fooled by this approach, myself included for a while. I finally decided that the approach is invalid since at no time do we deal with an actual closed circuit when evaluating the integral. In the OP's case it is valid for the complete semicircular circuit since the circuit is indeed closed, while the isolated wire is by definition not part of a closed circuit but just an artifice, an unrealizable concept. But this is an obvious ad hoc conclusion, not justified analytically, at least not for me.

What is even weirder to me is when I try to explain this by tracing ampere's law back to Maxwell's ∇ x H = j where j is current density. We then appeal to Stokes to get
∫∫(∇xH).dA = ∫H.dl = ∫∫j.dA = I.

Why does this sequence of arguments apply to the closed semicircular loop's straight wire but not to the isolated one? I guess the answer is the same as before: it applies only to realizable configurations, i.e. closed circuits since otherwise no current can be produced. But still it seems a bit of a copout. Isolated wires are often used as examples in texts. E.g. H. H. Skilling in his Fundamentals of Electric Waves uses it to exemplify computing a magnetic vector potential for a short wire. And an isolated wire is used as part of the solution to the OP's problem. So how does Biot-Savart apply to an impossible isolated current segment while ampere doesn't? Yet it's obvious that a B field around a very short wire would be lower than if the wire were long, carrying the same current.

@TSny - any help/comments appreciated.
@Tanya, sorry I know this doesn't address your concern. TSny can do that better than I or for that matter probably anyone else, so bear with him!

 

[Tanya Sharma]

You use Biot-Savart to find the magnitude and direction of B' on the path of integration due to the red current alone. You find that the direction of B' is counterclockwise as viewed from above.

Then $\small \oint \vec{B\:'} \cdot \vec{dl}$ $\small = \pm |B \: '|\; 2\pi R / \sqrt{3}$, where the sign will depend on whether you choose to integrate counterclockwise or clockwise around the path.

You then combine this result with the result for $\small \oint \vec{B \:''} \cdot \vec{dl}$ for the D-shaped loop (containing the blue current) which is easily found from Ampere's law. Of course you should integrate around the path in the same direction you chose for the red current. Here I have used the notation B'' for the field produced by the D-loop. (The field produced by just the black semicircular current alone is the vector sum of B' and B''.)

Please ignore my previous reply .

Here I will try to present my views in as simple terms as possible.

In the OP it is required to find $\oint \vec{B} \cdot \vec{dl}$ for the circular path , where $\vec{B}$ is the magnetic field due to semicircular current .

Instead I will use $\vec{B_1}$ for magnetic field due to semicircular current , $\vec{B_2}$ for magnetic field due to straight line current BA (blue) at the circular path, $\vec{B_3}$ for magnetic field due to straight line current AB (red) at the circular path.

If I consider clockwise positive then $\oint \vec{B_2} \cdot \vec{dl} = \frac{\sqrt{3}u_0I}{2}$ and $\oint \vec{B_3} \cdot \vec{dl} = -\frac{\sqrt{3}u_0I}{2}$

Since $\oint \vec{B_2} \cdot \vec{dl} = -\oint \vec{B_3} \cdot \vec{dl}$ as the magnetic field due to the two straight currents would be in opposite direction along the circular path , we superpose currents BA(blue) and AB(red) on the semicircular current so that $\oint \vec{B_1} \cdot \vec{dl} = \oint \vec{B_1} \cdot \vec{dl} + \oint \vec{B_2} \cdot \vec{dl}+\oint \vec{B_3} \cdot \vec{dl}$

Using Ampere’s Law $\oint (\vec{B_1}+ \vec{B_2}) \cdot \vec{dl} = u_0I$

Using Biot Savart Law we find $\vec{B_3}$ and then $\oint \vec{B_3} \cdot \vec{dl} = -\frac{\sqrt{3}u_0I}{2}$

Adding the above two , $\oint \vec{B_1} \cdot \vec{dl} + \oint \vec{B_2} \cdot \vec{dl}+\oint \vec{B_3} \cdot \vec{dl} = u_0I(1-\frac{\sqrt{3}}{2})$

Hence $\oint \vec{B_1} \cdot \vec{dl} = u_0I(1-\frac{\sqrt{3}}{2})$

Does this look better ?

 

[TSny]

What is even weirder to me is when I try to explain this by tracing ampere's law back to Maxwell's ∇ x H = j where j is current density. We then appeal to Stokes to get
∫∫(∇xH).dA = ∫H.dl = ∫∫j.dA = I.

Why does this sequence of arguments apply to the closed semicircular loop's straight wire but not to the isolated one? I guess the answer is the same as before: it applies only to realizable configurations, i.e. closed circuits since otherwise no current can be produced. But still it seems a bit of a copout. Isolated wires are often used as examples in texts. E.g. H. H. Skilling in his Fundamentals of Electric Waves uses it to exemplify computing a magnetic vector potential for a short wire. And an isolated wire is used as part of the solution to the OP's problem. So how does Biot-Savart apply to an impossible isolated current segment while ampere doesn't? Yet it's obvious that a B field around a very short wire would be lower than if the wire were long, carrying the same current.

I think these are good questions and I'm not sure I can answer them adequately.

If you consider a current in a wire as made up of a very large number of moving point charges, then the B field produced by these charges is the superposition of the fields due to each charge separately. The field of a moving point charge can be deduced from Maxwell’s equations (Lienard-Wiechert potentials, etc). As long as the speed of the charge is much less than c and as long as the acceleration of the charge is negligible, then the B field in the neighborhood of the point charge can be shown to reduce to the form $\frac{\mu_0}{4 \pi}\frac{ q\vec{v} \times \hat{r} }{r^2}$, to a good approximation. This expression is similar in form to the Biot-Savart law. In ordinary circuits carrying steady current, these assumptions are valid. Summing over all the charges in a current element, you get the Biot-Savart law for the element. The B field due to any finite section of a circuit is then found by integrating the Biot-Savart law over the elements of the section.

Ampere’s law can be derived from $\small \vec{\nabla} \times \vec{B} = \mu_0 \vec{j} + \mu_0 \varepsilon_0 \frac{\partial \vec{E}}{\partial t}$ under the assumption that the last term is negligible. That is, we assume that conditions are such that $\small \vec{\nabla} \times \vec{B} = \mu_0 \vec{j}$ is valid when deriving Ampere's law. Taking the divergence of both sides of this equation leads to the requirement that $\small \vec{\nabla} \cdot \vec{j} = 0$. But, if we take a section of a circuit as in Tanya’s question, we do not have $\small \vec{\nabla} \cdot \vec{j} = 0$ at the two end points of the section. So, $\small \vec{\nabla} \times \vec{B} = \mu_0 \vec{j}$ is not true for this isolated section of current. Ampere’s law will not generally hold for an isolated finite section of current.

 

[TSny]

Does this look better ?

Yes. That looks very good!

 

[rude man]

Taking the divergence of both sides of this equation leads to the requirement that $\small \vec{\nabla} \cdot \vec{j} = 0$. But, if we take a section of a circuit as in Tanya’s question, we do not have $\small \vec{\nabla} \cdot \vec{j} = 0$ at the two end points of the section. So, $\small \vec{\nabla} \times \vec{B} = \mu_0 \vec{j}$ is not true for this isolated section of current. Ampere’s law will not generally hold for an isolated finite section of current.

This is a new thought for me. Seems very appurtenant. Thanks TS.

 

[TSny]

appurtenant

My new word of the day . Thanks.

 

[rude man]

My new word of the day . Thanks.

Ho ho! Small repayment for your elucidations!
Next time I'll use 'apposite'!

rm

 

[Tanya Sharma]

Yes. That looks very good!

Thanks :)

Suppose in the OP instead of a semicircular conductor ,we were given a D shaped conductor carrying current similar to what we had when we considered the blue shaped current BA + semi circular current .Now we were asked to calculate $\oint \vec{B_1} \cdot \vec{dl}$ for the circular path 3x² +3z² =R²,where $\vec{B_1}$ is the magnetic field due to semi circular current .

Here is what I think :

Suppose $\vec{B_2}$ is the magnetic field due to straight line current BA (blue) at the circular path .

Using Ampere's Law $\oint (\vec{B_1}+ \vec{B_2}) \cdot \vec{dl} = u_0I$ .

Using Biot Savart Law we find $\vec{B_2}$ and then $\oint \vec{B_2} \cdot \vec{dl} = \frac{\sqrt{3}u_0I}{2}$

Subtracting the second relation from the first one , we have , $\oint \vec{B_1} \cdot \vec{dl} + \oint \vec{B_2} \cdot \vec{dl}-\oint \vec{B_2} \cdot \vec{dl} = u_0I(1-\frac{\sqrt{3}}{2})$

Hence $\oint \vec{B_1} \cdot \vec{dl} = u_0I(1-\frac{\sqrt{3}}{2})$ .

This is the same relation we had obtained when we were using superposition principle to find the $\oint \vec{B_1} \cdot \vec{dl}$ when only semicircular current was given .

Doesn't this mean that the semicircular current is equivalent to D shaped current as far as calculating the value of $\oint \vec{B_1} \cdot \vec{dl}$ is considered ?

If this is true then what I said in post#6 seems correct .

What do you say ?

 

[TSny]

Yes, everything looks good. I was misinterpreting how you were using the word "equivalent". I thought you were implying that the semicircle current (alone) and the D loop produce the same result for the integral of B_net around the circular path.

What if you replaced the semicircular current from A to B with a current of a different shape, such as shown in the attachment?

 

[Tanya Sharma]

What if you replaced the semicircular current from A to B with a current of a different shape, such as shown in the attachment?

a) $\oint \vec{B} \cdot \vec{dl} = u_0I(1-\frac{\sqrt{3}}{2})$

b) $\oint \vec{B} \cdot \vec{dl} = \frac{\sqrt{3}}{2}u_0I$

c) $\oint \vec{B} \cdot \vec{dl} = u_0I(1+\frac{\sqrt{3}}{2})$

Lets see how much I score in the test .