I Amplitude of the maximums in single slit diffraction

[jaumzaum]

Hello!

I was trying to calculate the amplitude of the secondary maximums in the single slit diffraction.
When I use the formula:
$$ I = I_0 (\frac {sin(\Delta \phi /2)} {\Delta \phi /2})^2 $$
If I take $x = \Delta \phi /2$ and derivate I get that the maximum occurs when:
$$ x = tan(x) $$
The first 2 solutions are x=± 4.493409 and x=± 7.72525
which gives $I_0/I$= 21.19 and 60.68 respectively.

However, this site gives a more direct way of calculating the maximums.
They say the first secondary maximum occurs when the phasors make 1 and a half loop, and the second secondary maximum when the phasors make 2,5 loop. However, that gives a slight different answer, 22.21 and 61.68 respectively
View attachment 323616

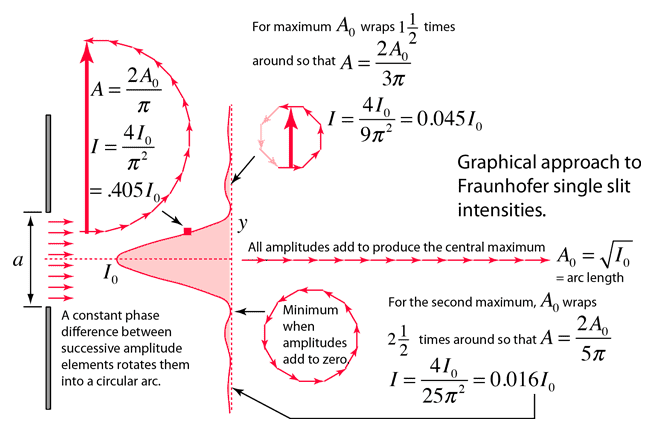
Why are the values different? Which one is right?

Thanks!

 

[Steve4Physics]

Why are the values different? Which one is right?

Not my area but I believe neither answer is correct! (Though they’re accurate enough for most purposes.)

I think the equations you are using are (pretty good) approximations. But there will be some small inaccuracies.

The ‘exact’ intensity distribution (if Wikipedia is to be trusted) is:$$I(\theta) = I_0 \left[ sinc \left( \frac {\pi a}{\lambda} \sin \theta \right) \right]^2$$(The ‘$sinc$’ function is defined as $sinc(x) = \frac {\sin(x)}x$.)

You’d have to differentiate that to find the angles of the maxima. (Note the plural of ‘maximum’ is ‘maxima’!)

https://en.wikipedia.org/wiki/Diffraction_from_slits#Single_slit

Maybe someone with a more in-depth knowledge will be able to provide more detail.

 

[jaumzaum]

Not my area but I believe neither answer is correct! (Though they’re accurate enough for most purposes.)

I think the equations you are using are (pretty good) approximations. But there will be some small inaccuracies.

The ‘exact’ intensity distribution (if Wikipedia is to be trusted) is:$$I(\theta) = I_0 \left[ sinc \left( \frac {\pi a}{\lambda} \sin \theta \right) \right]^2$$(The ‘$sinc$’ function is defined as $sinc(x) = \frac {\sin(x)}x$.)

You’d have to differentiate that to find the angles of the maxima. (Note the plural of ‘maximum’ is ‘maxima’!)

https://en.wikipedia.org/wiki/Diffraction_from_slits#Single_slit

Maybe someone with a more in-depth knowledge will be able to provide more detail.

Thanks @Steve4Physics

That is the exact same equation I am using.

Where $\Delta \phi = \frac {2\pi a sin\theta}{\lambda}$

 

[Steve4Physics]

That is the exact same equation I am using.

Where $\Delta \phi = \frac {2\pi a sin\theta}{\lambda}$

Aha! I misinterpreted the meaning of $\Delta \phi$. (It wasn't defined in Post #1.)

So intensity as a function of $\theta$, expressed without the '$sinc$' and $\Delta \phi$ is:$$I(\theta) = I_0 \left[
\frac
{\sin \left( \frac {\pi a}{\lambda} \sin \theta \right)}
{\left( \frac {\pi a}{\lambda} \sin \theta \right)}
\right]^2$$To find a maximum intensity we need the value of $\theta$ which makes $\frac {dI}{d\theta} = 0$ and $\frac {d^2I}{d\theta^2} < 0$.

Assuming your solution for this is correct, we only need to explain why the 'phasor' method is slightly inaccurate.

It appears that when doing the phasor-addition, it is only an approximation (but a good one) to assume the phasors line-up along a perfectly cicular arc. But it turns out the arc is not perectly circular.

A quick search produced this (concerning the 1st two maxima). See link below for context:

“These two maxima actually correspond to values of ϕ slightly less than 3π rad and 5π rad. Since the total length of the arc of the phasor diagram is always NΔE0, the radius of the arc decreases as ϕ increases. As a result, E1 and E2 turn out to be slightly larger for arcs that have not quite curled through 3π rad and 5π rad, respectively. “​

​

About halfway down https://phys.libretexts.org/Bookshe...on/4.03:_Intensity_in_Single-Slit_Diffraction