OJFord
- 29
- 0
Hi, unless I'm missing something here, it seems to me that the answer is that it is infinite, and that that is pretty intuitive.
Is that not the case?
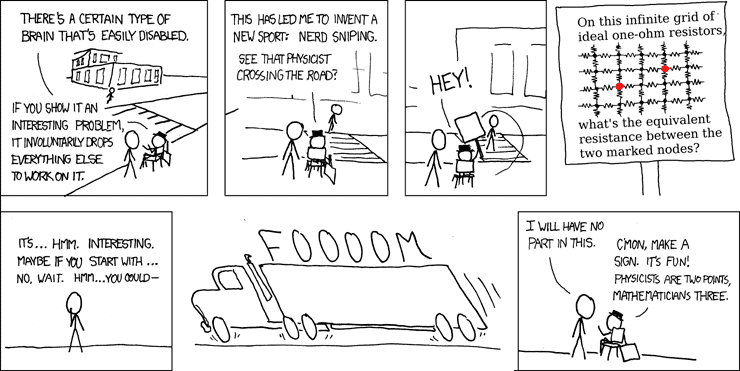
I would think it could be simplified to view as two parallel and infinite resistances, giving ∞2/2∞, which simplifies to half infinity, which is of course really (in as much as it is) still infinite.
Is that not the case?
I would think it could be simplified to view as two parallel and infinite resistances, giving ∞2/2∞, which simplifies to half infinity, which is of course really (in as much as it is) still infinite.