- 1,047
- 785
Veritasium on YouTube https://www.youtube.com/c/veritasium/community has posted this problem, inviting viewers to say what would happen:
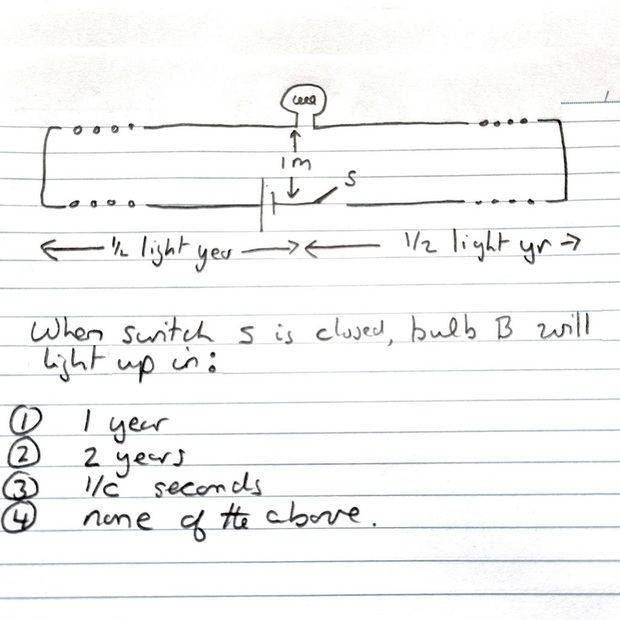
Is the following answer correct?
Is the following answer correct?
In series with the battery, switch and lamp are two transmission lines. At ##t = 0^+##, we will have twice the characteristic impedance ##2Z_0## of the line in series with the lamp. Since the wire spacing is 1 meter, ##2Z_0## would be quite large, which will limit the current and won't let the lamp glow. Once the voltage steps make one round trip (simultaneously) though the left and right lines, the series impedance will drop to zero and the lamp will light up.
But if we replace the lamp with a neon lamp or an LED, and use a high enough voltage, then the lamp would light up instantly because then the ##2Z_0## would be less than the lamp resistance.
But if we replace the lamp with a neon lamp or an LED, and use a high enough voltage, then the lamp would light up instantly because then the ##2Z_0## would be less than the lamp resistance.
Last edited: