- #1
DaveC426913
Gold Member
- 22,497
- 6,168
- TL;DR Summary
- This question appeared on the American SAT test until recently removed. Can you solve it?
Fascinating, and utterly unintuitive.
This is a question that appeared on the American SAT test until it was recently removed. (citation: Veritasium, to which I will not link at this time.)
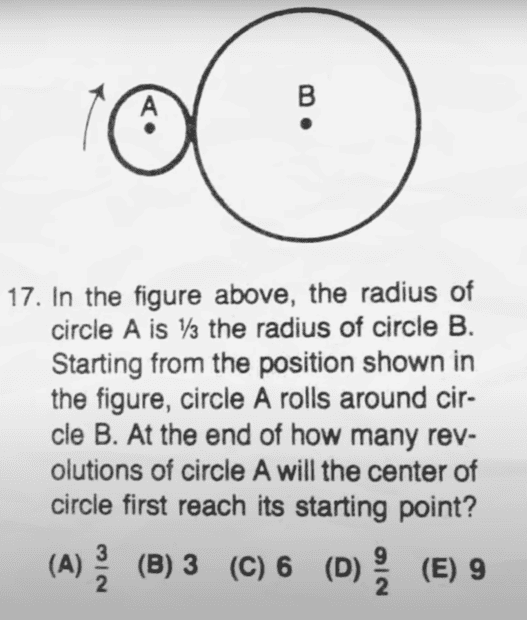
Every student ever has gotten it wrong, and that's because the SAT writers got it wrong too. The correct answer is not listed at all.
And I guarantee that, even knowing this, you will get it wrong too (unless you cheat, or unless you are a PF-regular - IOW, a super-genius at math).
I got it wrong, and I can hardly believe it even after having been shown the correct answer.
Feel free to post your answers using the spoiler tag.
This is a question that appeared on the American SAT test until it was recently removed. (citation: Veritasium, to which I will not link at this time.)
Every student ever has gotten it wrong, and that's because the SAT writers got it wrong too. The correct answer is not listed at all.
And I guarantee that, even knowing this, you will get it wrong too (unless you cheat, or unless you are a PF-regular - IOW, a super-genius at math).
I got it wrong, and I can hardly believe it even after having been shown the correct answer.
Feel free to post your answers using the spoiler tag.

