The What and Why of Circuit Analysis Assumptions

Probably everyone reading this article already has education on elementary circuit analysis (CA) and many of us are much more advanced. Typically, the basic course covers both circuits covers simple devices like R, L, and C, it mentions electric or magnetic fields, then moves on to Ohm’s Law and CA… But few such courses explicitly define the boundary between CA and those other electric topics. The result is that many experts never do learn about that boundary.

Quantum Electrodynamics (QED), Maxwell’s Equations or Field Theory (FT), and CA are the only accurate and internally consistent levels typically used to analyze electric things. Usually, only researchers delve into the quagmire between those three safe-havens. QED is the most general and accurate whereas. CA is the broadest and pragmatic method applicable for circuits of huge scale and complexity. In my own field, power engineering, we routinely use CA to find both steady-state and transient solutions for electric circuits of continental scale, including representations of everything connected to those grids.

The Three Assumptions of CA

The Wikipedia article lumped element model explains them clearly as do these lecture notes based on the Nilsson Reidel textbook Electric Circuits. My own comments are in italics.

1. The time rate of change of magnetic flux outside any conductor is zero. [$\frac{\partial{\phi_B}}{\partial{t}}=0$]
   If the initial flux at t=0 was zero, it remains zero. [So basically forget magnetic flux for CA. Forget Poynting vectors.]
2. The time rate of change of electric charge inside any conductor is zero. [$\frac{\partial{q}}{\partial{t}}=0$]
   If the initial static charge in the circuit was zero, it remains zero. [So basic[ally forget to charge and the flow of charge in CA. ]
3. The time scales of interest in CA are much larger than the end-to-end propagation delay of electromagnetic waves in the conductors.
   [Also called the quasi-stationary assumption.],[Here is a simple benchmark. The wires in 60 hertz AC circuits should be less than 500 km long.]

The implications are:

• No electric fields.
• No magnetic fields.
• No electric charges.
• Kirchoff’s Laws apply instantaneously around the entire circuit, so there is no temporal first-next ordering of events.

In my opinion, this is where many basic courses fail us. Having just taught that capacitors work via electric fields, and that inductors and transformers work via magnetic fields and that all that depends on the motion of electron charge carriers, it should be emphasized that both fields and charges must be ignored for CA. Instead, the assumptions may not even be mentioned.

CA also rules out pop-sci explanations such as “First apply the voltage, then the current flows, because electrons need time to accelerate.” That would violate Kirchoff’s Laws, so it is excluded in CA.

The Benefits of CA

But more importantly, where those assumptions are valid, we can employ a vast host of analytical tools.

1. Kirchoff’s Voltage Law (KVL), and Kirchoff’s Current Law (KCL)
2. Linear ideal components, R, L, and C, the diode, ideal transformer, ideal voltage source V, ideal current source I.
3. Series and parallel combinations, superposition, impedance transform.
4. Complex phasors, and symmetrical components.
5. Theorems: Thevanin’s, Norton’s, Millman’s, Tellgen’s
6. Methods: Nodal analysis, mesh analysis, matrices, sparse matrices, time domain, frequency domain, Laplace transforms, Lagrangians, Hamiltonians, tensors, and diakoptics,

Are you surprised to see that plain old circuit analysis gets as advanced as tensors and diakoptics? Then study the work of the legendary engineer Gabriel Kron.

Last but not least, CA allows us to layout our diagrams and circuits freely without changing their behavior. For example, the following three circuits are the same using CA, but most certainly not alike to Maxwell’s Equations.

The same applies to the circuits in the pictures below. One is just a conceptual schematic, one built manually with a soldering iron, and one built by robots with printed circuits. All three can in principle be identical for CA purposes, provided that we check that the assumptions are not violated. Cross-talk is a possible violation. Those physical circuits would be exceedingly hard to analyze using more rigorous Maxwell’s Equations and harder still using QED.

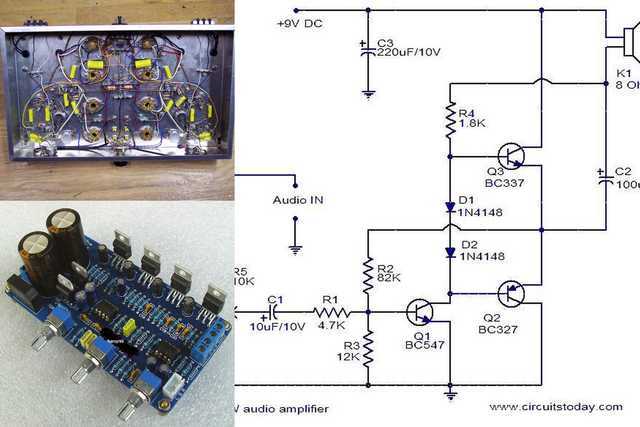
It is hard to imagine today’s electric and electronic industries even existing if we did not have the analytical power of CA at our disposal. It is only in special circumstances that the industry needs FT or QED analysis.

Pragmatic Modeling

Modeling (simulation) of physical systems is a two-step process. Step 1 is writing the equations that represent the physics. Step 2 is solving those equations. CA is the step 2 part of the process. It is a purely mathematical process, divorced from physics. The CA tools mentioned above are mathematical tools. Analysts are thus better off focusing on the analysis task and ignoring the physics.

It is tempting to think that idealized components (R, L, C, V, I, diode, transformer) are merely simplified versions of the real things. For example, an L is just an inductor where we neglect any resistance and parasitic capacitance it has in real life. But at the CA stage, we focus on the analysis. For example, in CA L is simply a $\frac{dI}{dt}$ term, nothing more.

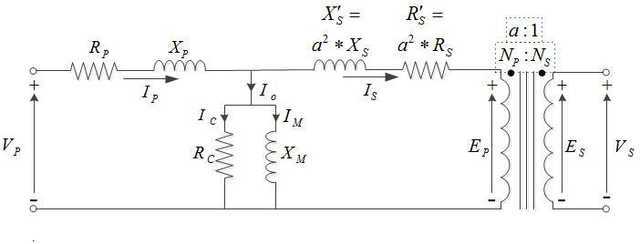
It is common practice to model real-life components using equivalent circuits of ideal components. For example, a real-life transformer violates the assumptions of CA, but the transformer equivalent circuit below (which includes an ideal transformer) complies with CA assumptions.

Why Are These Assumptions Unfamiliar to Many Experts?

Understandably, we teach many students topics in the order simplest-first. [I’m sure there are exceptions to that.] If we teach CA first, then FT second and QED last, where is the logical place to insert these assumptions? Before CA they make little sense. After FT they seem moot. But if we taught in the order fundamental first to pragmatic last, we would start with QED, then FT, and CA last. Injecting the assumptions after FT and before CA would be natural. So, it is my opinion that these assumptions get lost as a consequence of our teaching methods.

Dealing With Conduction Questions on PF

A recurring problem on PF is raised by students who may have learned about components and CA and wish to go a “little bit” deeper to understand electrical conduction. To make it worse, many are unwilling to go further with serious study and unwilling to deal with math beyond what they already know. Sometimes, the tip-off is when the student mentions electrons.

On the other hand, we have PF veterans who wish to help these students while avoiding pop-sci or lame analogies. How should we respond?

Let’s examine the problem. One can be an A-level student or even a professional using CA and FT without any mention of electrons. [Vacuum tubes, P-N junctions, Van de Graff, particle accelerators, and electric arcs are exceptions that do require explicit consideration of individual electrons.] It is at the quantum level where electrons become an essential part of the picture. Indeed, the correct description of conduction in my opinion is presented in the Wikipedia article Free Electron Model (which supersedes the earlier Drude Model). The article uses a mix of FT and crystallography, with quantum effects. It is difficult material requiring extensive prior study to understand.

So the answer seems to be a bitter pill. To the student question, “Can’t I go just a little bit deeper to understand conduction in a wire?” the correct answer is “No.” Most of us like to encourage inquisitiveness, so we hate saying no. But the laws of physics are not arranged to suit our convenience. Sometimes tough love is the best approach.