An iron cylinder inside a solenoid

[lorenz0]

Homework Statement:

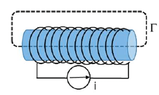
An iron cylinder with section $S = 10 cm^2$ and length $d = 20 cm$ is uniformly magnetized being placed into a solenoid with $200$ turns around the surface of the cylinder and traversed by a current $i$. The magnetic field that is measured inside the cylinder is $H = 10^3 A / m$ and $\oint_{\Gamma} \vec{B}\cdot d\vec{l}= 8\cdot 10^{-4} T m$.
Calculate the current $i$ flowing in the circuit and the magnetization vector $\vec{M}$.

Relevant Equations:

$\oint_{\Gamma}\vec{H}\cdot d\vec{l}=\sum I$, $\vec{H}=\frac{\vec{B}-\mu_0\vec{M}}{\mu_0}$

From $\oint_{\Gamma}\vec{H}\cdot d\vec{l}=\sum I$ by Ampere's Law which gives $H \Delta l=\Delta N\cdot i\Leftrightarrow H=n i$ where $n=$ number of turns per unit length so $i=\frac{H}{n}=\frac{10^3 A / m}{\frac{200}{0.2m}}=1 A$.

Since $\vec{H}=\frac{\vec{B}-\mu_0\vec{M}}{\mu_0}$ we also get $\oint_{\Gamma}\vec{H}\cdot d\vec{l}=\frac{1}{\mu_0}\oint_{\Gamma}(\vec{B}-\mu_0\vec{M})\cdot d\vec{l}\Leftrightarrow \oint_{\Gamma}\vec{M}\cdot d\vec{l}=\frac{1}{\mu_0}\oint_{\Gamma}\vec{B}\cdot d\vec{l}-ni\Leftrightarrow M=\frac{1}{\mu_0}\oint_{\Gamma} \vec{B}\cdot d\vec{l}-\frac{n}{l}i=\frac{1}{4\pi\cdot 10^{-7} H/m}\cdot (8\cdot 10^{-4}Tm)-\frac{200}{0.2m}1 A$ ... this last part doesn't really convince me, even dimensionally, even if it looks like the initial idea to use Ampere's Law and then make the substitution $\vec{H}=\frac{\vec{B}-\mu_0\vec{M}}{\mu_0}$ does make sense?

Is there a way to amend my work? I would like to understand how to work with magnetic fields in matter like in this case and I would be grateful for an explanation about how to do that. Thanks

 

[Charles Link]

This one doesn't seem to be the best problem of this type. The numbers for $B$ are too small, and both $H$ and $B$ will not be constant along the loop $\Gamma$ shown for the integral. It looks like you computed the current $i$ correctly, but I don't know that much else can be done with the numbers they give you.

In addition, the magnetic field that gets measured is $B$. The "field" $H$ does not get measured unless you measure $B$ without the iron in the solenoid. It is also incorrect to say that $\oint B \cdot dl$ was measured, unless a complete mapping was done.

I don't know of a very good way of treating the finite length iron cylinder inside a solenoid, unless you are given the value of the magnetization $M$ and or the value of $B$ in the iron. Writing $\oint H \cdot dl=NI$ does not lead to a straightforward solution, because $H$ is very non-uniform. Complex numerical methods using the pole method could be useful, but that is a somewhat advanced treatment of the problem, and would take a lot of work.

 

[lorenz0]

This one doesn't seem to be the best problem of this type. The numbers for $B$ are too small, and both $H$ and $B$ will not be constant along the loop $\Gamma$ shown for the integral. It looks like you computed the current $i$ correctly, but I don't know that much else can be done with the numbers they give you.

In addition, the magnetic field that gets measured is $B$. The "field" $H$ does not get measured unless you measure $B$ without the iron in the solenoid. It is also incorrect to say that $\oint B \cdot dl$ was measured, unless a complete mapping was done.

I don't know of a very good way of treating the finite length iron cylinder inside a solenoid, unless you are given the value of the magnetization $M$ and or the value of $B$ in the iron. Writing $\oint H \cdot dl=NI$ does not lead to a straightforward solution, because $H$ is very non-uniform. Complex numerical methods using the pole method could be useful, but that is a somewhat advanced treatment of the problem, and would take a lot of work.

Thanks for your very thorough answer

 

[Charles Link]

I gave it a little more thought: To a somewhat good approximation, you could assume that $B\approx 0$ in the exterior part of the loop for the integral. This is not ideal, but it could work for some estimates. In any case, $B$ in the iron should be in the neighborhood of $1$ T, (considering the value of $H$ and typical magnetic susceptibility values for iron), so that the integral $\oint B \cdot dl$ should be about .2 Tm. This is where the problem is really lacking, and without a better number for the integral, it limits us in what we can do with it.

 

[Charles Link]

It is perhaps worthwhile to mention a couple additional things about this problem. It seems to not be treated in detail in a lot of the E&M textbooks. In the case of iron, such as that which is used in transformers, the hysteresis curve is such that when the applied $H$ from the solenoid is just slightly negative (approximately zero), the magnetization $M$ will also be zero. Meanwhile for material that would make a permanent magnet, the applied $H$ needs to be very large and negative to reverse the direction of magnetization.

One other thing worth mentioning is that the magnetization will saturate in the iron at somewhere around $\mu_o M=2$ T. With the numbers that were given here for $H$, I believe the $M$ would be rather close to saturation, rather than giving a number that they gave for $\oint B \cdot dl$ of $8E-4$ with an $L=.2$.

The available literature on the subject of permanent magnets as well as the case of iron in a solenoid that makes an electromagnet seems to have improved in the last couple of years, but previous to that, it seemed to be rather deficient.