Analysis of Verlet integration method

[woodssnoop]

Hello:

I am trying to determine the global error for the verlet integration algorithm: $r_{i+1}=2r_{i}-r_{i-1}+\ddot{r}_{i}h^{2}$
It is easy to show that this approximation is locally 4th order, by way of a Talyor expansion. I have look around extensively for a proof of the global error but have been unsuccessful in finding a reasonable derivation anywhere (the articles I have found seem to make too many unjustified assumption and/or glaze over the dropping of terms; similar to the wikipedia page on verlet integration). (1) Has anyone else ran across a good derivation of the verlet integrators global error? My attempts at finding the global error for this expression has proved to be quite difficult.

The numerical testing I have done has shown 2nd order global error, but I can't prove it. (2) I know I have to show that $d_{k} \leq M n^2$ for all $k \leq n$, where M is some constant, but how can I show this for an arbitrary M? In real analysis, you show an equation like this is true by showing that for any $\epsilon$ you can find a $n$ such that the expression holds, but I can't seem to frame my problem in those terms. I have been trying several different approaches, and my latest attempt is below.



My first step was to set up a difference equation for $r_{i}$ and $r(h*i)$ where $r(h*i)$ is the exact solution and $r_{i}$ is the approximate solution. After subtracting the two expression I get the difference formula:
$d_{i+1}=2d_{i}-d_{i-1}-h^{2}(\ddot{r}_{i}-\ddot{r}(h*i)) - O(h^{4})$

using the mean value theorem:
$d_{i+1}=2d_{i}-d_{i-1}-h^{2}(\ddot{\xi}_{i}d_{i}) - O(h^{4})$ for $\xi\in[r_{i},r(h*i)]$

$\Leftrightarrow d_{i+1}-(2-h^{2}(\ddot{\xi}_{i}))d_{i}+d_{i-1}=-O(h^{4})$

$r$ is differentiable on the interval $[0,h*n]$. Which implies $\ddot{\xi}_{i}$ has a maximum. Letting $\epsilon=h^{2}\ddot{\xi}_{i}$ gives:

$d_{i+1}-(2-\epsilon)d_{i}+d_{i-1}=-O(h^{4})$

condensing further:

$d_{i+1}-xd_{i}+d_{i-1}=-O(h^{4})$ where $x=2-\epsilon$.

This expression can be written out in matrix form (shown below is just a 12X12 example) where A=

Taking the inverse of A yields:

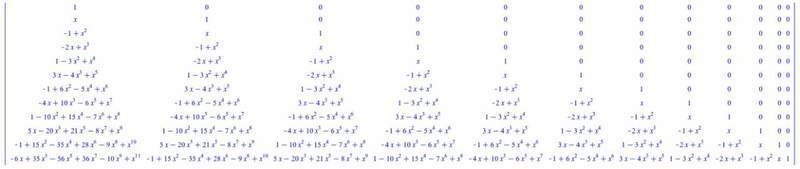
The rows of A have a closed form solution:
$a(i)=\frac{(x-\sqrt{x^{2}-4})^{i}-(x-\sqrt{x^{2}-4})^{i}}{2^{i}\sqrt{x^{2}-4}}$

$\Rightarrow d_{n}=\sum_{i=1}^{n}a(i)$

This two can be expressed in a better way:
$d_{n}=\frac{(\frac{x-\sqrt{x^{2}-4}}{2})^{n}(\sqrt{x^{2}-4}+x-2)+(\frac{x+\sqrt{x^{2}-4}}{2})^{n}(\sqrt{x^{2}-4}-x+2)-2\sqrt{x^{2}-4}}{x-2}$

I am trying to show that $d(n) \leq M n^2$, but I have been having trouble show that this true.

 

[AlephZero]

Personally I would use a different approach to investigating the global error.

The local error for a single step doesn't tell you much, because it assumes that all the "input" quantities are exact. But when you take the second step, that assumption is false.

The idea of a global error estimate only really makes sense given some restrictions on the function you are integrating. I've never used Verlet integration for "real work" but I bet it is possible to invent an ODE where the error is order (1), or it even goes unstable, for any constant size step. But of course if you wanted to integrate such an equation. you wouldn't use Verlet...

So, I would start by looking at the global behavior for a simple ODE, say x'' + x = 0.

Any exact solution is a linear combination of the two independent solutions $x = e^{i t}$ and $x = e^{-i t}$, where the linear combination depends on the boundary conditions. (It's easier to work with complex solutions, even if in "real life" you are only interested in real solutions)

To compare the exact solution with with the finite difference solution, write the FD equations in the form
$$\left[ \begin{matrix} x_{i+1} \cr x_i \end{matrix}\right] = \left[ A \right] \left[\begin{matrix} x_i \cr x_{i-1} \cr \end{matrix}\right]$$
where A is a 2x2 matrix.

$$A = \left[ \begin{matrix} 2-h^2 & -1 \cr 1 & 0 \end{matrix}\right]$$

The first row of A represents the FD scheme for the test equation (using the fact that x'' = -x), the second row just says $x_i = x_i$.

Now, find the eigenvalues and vectors of A. They will represent two "basic solutions" of the FD scheme, which should be oscillating functions that tend to the solutions of the ODE in te limit as h goes to 0. The difference between the FD and ODE solutions will give you a measure of the global error.

Hope that helps.

 

[woodssnoop]

Personally I would use a different approach to investigating the global error.

The local error for a single step doesn't tell you much, because it assumes that all the "input" quantities are exact. But when you take the second step, that assumption is false.

The idea of a global error estimate only really makes sense given some restrictions on the function you are integrating. I've never used Verlet integration for "real work" but I bet it is possible to invent an ODE where the error is order (1), or it even goes unstable, for any constant size step. But of course if you wanted to integrate such an equation. you wouldn't use Verlet...

So, I would start by looking at the global behavior for a simple ODE, say x'' + x = 0.

Any exact solution is a linear combination of the two independent solutions $x = e^{i t}$ and $x = e^{-i t}$, where the linear combination depends on the boundary conditions. (It's easier to work with complex solutions, even if in "real life" you are only interested in real solutions)

To compare the exact solution with with the finite difference solution, write the FD equations in the form
$$\left[ \begin{matrix} x_{i+1} \cr x_i \end{matrix}\right] = \left[ A \right] \left[\begin{matrix} x_i \cr x_{i-1} \cr \end{matrix}\right]$$
where A is a 2x2 matrix.

$$A = \left[ \begin{matrix} 2-h^2 & -1 \cr 1 & 0 \end{matrix}\right]$$

The first row of A represents the FD scheme for the test equation (using the fact that x'' = -x), the second row just says $x_i = x_i$.

Now, find the eigenvalues and vectors of A. They will represent two "basic solutions" of the FD scheme, which should be oscillating functions that tend to the solutions of the ODE in te limit as h goes to 0. The difference between the FD and ODE solutions will give you a measure of the global error.

Hope that helps.

My PI was able to find a reference for the 2nd order convergence, since the verlet algorithm can also be thought of as a version of the midpoint formula. The reference is from "An Introduction to Numerical Analysis, Second Edition" by Kendall E. Atkinson.

Thanks for your help.

 

[AlephZero]

At first glance, I couldn't see the difference between the Verlet algorithm and what used to be called the Central Difference method - maybe that is now called the midpoint method?

But I don't know much about Verlet except what it says in Wikipedia, and I don't believe everything I read there!