Discussion Overview
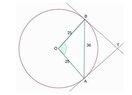
The discussion revolves around the calculation of the angle between the tangents to a circle, specifically focusing on a problem where the angle T is stated to be approximately 87.9 degrees. Participants seek clarification and different methods for evaluating this angle using geometric principles.
Discussion Character
- Technical explanation, Mathematical reasoning, Homework-related
Main Points Raised
- Some participants request further explanations regarding the calculation of angle T, which is given as 87.9 degrees.
- One participant suggests using the cosine rule and notes that the radii and tangents to a circle are always perpendicular, implying a relationship between the angles in the quadrilateral OBTA.
- Another participant outlines a method involving the bisection of triangle ABO, the Pythagorean theorem, and the law of sines to derive angle T, providing a detailed step-by-step approach.
- The outlined method concludes with an expression for angle T, approximating it to 87.89 degrees, indicating a slight variation from the previously stated angle.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the method for calculating angle T, as multiple approaches are presented, and the exactness of the angle remains a point of discussion.
Contextual Notes
Some assumptions regarding the geometric properties of circles and the relationships between angles in triangles and quadrilaterals are present but not explicitly stated. The discussion includes varying methods and approximations for angle T.