Angular momentum after a collision

[Jenny Physics]

Homework Statement

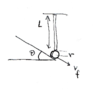
A disk of radius $r$ and mass $m$ rolls down an inclined plan. It reaches the end of the plane with velocity $v_{f}$ and collides with a vertical rod of length $L$ and mass $M$ sticking with it. See figure.

What is the angular momentum magnitude and direction after the collision?

Homework Equations

$$L=I_{disk}\omega$$

The Attempt at a Solution

The moment of inertia of the disk relative to the pivot is (using the parallel axis theorem)
$$I_{disk}=\frac{1}{2}mr^{2}+m(L+r)^{2}$$.
Angular momentum is conserved. The initial (and hence the final i.e. right after the collision) angular momentum is

$$L_{initial}=I_{disk}\omega=I_{disk}\frac{v_{f}\cos\theta}{L+r}=m\left[\frac{1}{2}mr^{2}+m(L+r)^{2}\right]\frac{v_{f}\cos\theta}{L+r}$$

Angular momentum points out of the plane since rotation is counterclockwise

However the solution is different . Where am I wrong?

 

[TSny]

$$L=I_{disk}\omega$$ $$I_{disk}=\frac{1}{2}mr^{2}+m(L+r)^{2}$$.

These two equations would be applicable only if the disk is in pure rotation about the pivot point (at the top of the rod). But this is not the type of motion that the disk has just before the collision. There is a general theorem for the angular momentum of a rigid body that you can use. See, for example, the equation in the box in the section "The Angular Momentum of a Rigid Object Rotating and Translating" at this link
https://scripts.mit.edu/~srayyan/PE...of_a_Rigid_Body_both_Rotating_and_Translating