brotherbobby
- 755
- 170
Statement of the problem :
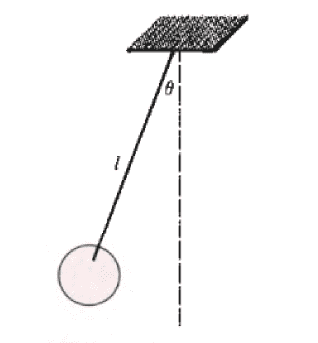
A ball shown in the figure is allowed to swing in a vertical plane like a simple pendulum. Answer the following :
(a) Is the angular momentum of the ball conserved?
No, the angular momentum ##L = mvl##, where m is the mass of the ball and v is its speed at an instant. Note, this is an example of (non-uniform) circular motion whereby vector v ##\perp## radius vector r at all instants. Clearly, v changes, reaching its maximum value when ##\theta = 0## and hence the angular momentum L also changes, becoming maximum at the mean position.
(b) Calculate the direction of L at some time. Does it change?
No. The motion takes place in a plane. From the definition of L = r ##\times## p, using either the right hand cork screw rule or taking the convenient mean position of the pendulum to evaluate (r ##\rightarrow - \hat y##, p ##\rightarrow \hat x##, ##-\hat y \times \hat x = \hat z##), we find that the direction of L is along the +z axis, out of the page.
(c) What force acting on the pendulum gives a zero torque about an axis perpendicular to the motion plane and through the point of support?
Tension T. By the definition of torque, ##\tau = r \times F \Rightarrow \tau = l \hat l \times -T \hat l = 0##, where ##\hat l## is the unit vector along the rope out from the point of support.(d) Calculate the torque due to the weight of the ball about this axis at an angle ##\theta##.
From definition, ##\tau = r \times F##. At the angle ##\theta##, the only contributing force to the torque is the "vertical" component of weight, ##mg \sin \theta## (The tension and the "horizontal" component of weight ##mg \cos \theta## both lie along the rope). Hence the magnitude of torque ##\mathbb{\tau = mg \sin \theta l}##. (e) Calculate the magnitude of the rate of change of angular momentum of the pendulum bob at ##\theta##.
If ##L = mvl## [see (a)], then ##\frac {dL} {dt} = m \frac {dv} {dt} l = m g \sin \theta l = mgl \sin \theta##, as the rate of change of v, ##\frac {dv}{dt} = g \sin \theta##, in a direction perpendicular to the rope and along the motion of the bob.
Thank you for you interest.
A ball shown in the figure is allowed to swing in a vertical plane like a simple pendulum. Answer the following :
(a) Is the angular momentum of the ball conserved?
No, the angular momentum ##L = mvl##, where m is the mass of the ball and v is its speed at an instant. Note, this is an example of (non-uniform) circular motion whereby vector v ##\perp## radius vector r at all instants. Clearly, v changes, reaching its maximum value when ##\theta = 0## and hence the angular momentum L also changes, becoming maximum at the mean position.
(b) Calculate the direction of L at some time. Does it change?
No. The motion takes place in a plane. From the definition of L = r ##\times## p, using either the right hand cork screw rule or taking the convenient mean position of the pendulum to evaluate (r ##\rightarrow - \hat y##, p ##\rightarrow \hat x##, ##-\hat y \times \hat x = \hat z##), we find that the direction of L is along the +z axis, out of the page.
(c) What force acting on the pendulum gives a zero torque about an axis perpendicular to the motion plane and through the point of support?
Tension T. By the definition of torque, ##\tau = r \times F \Rightarrow \tau = l \hat l \times -T \hat l = 0##, where ##\hat l## is the unit vector along the rope out from the point of support.(d) Calculate the torque due to the weight of the ball about this axis at an angle ##\theta##.
From definition, ##\tau = r \times F##. At the angle ##\theta##, the only contributing force to the torque is the "vertical" component of weight, ##mg \sin \theta## (The tension and the "horizontal" component of weight ##mg \cos \theta## both lie along the rope). Hence the magnitude of torque ##\mathbb{\tau = mg \sin \theta l}##. (e) Calculate the magnitude of the rate of change of angular momentum of the pendulum bob at ##\theta##.
If ##L = mvl## [see (a)], then ##\frac {dL} {dt} = m \frac {dv} {dt} l = m g \sin \theta l = mgl \sin \theta##, as the rate of change of v, ##\frac {dv}{dt} = g \sin \theta##, in a direction perpendicular to the rope and along the motion of the bob.
Thank you for you interest.
