Angular Velocity: Calculating Revolutions in 4 Seconds
- Thread starter StephenDoty
- Start date
Click For Summary
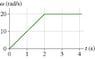
To determine the number of revolutions made by an object in 4 seconds, the area under the angular velocity versus time graph is crucial, totaling 60. The discussion revolves around whether to convert this area directly into revolutions using the formula 60/2π or to sum the angular velocities at each second, which yields a total of 70. Clarification on the appropriate method for calculating revolutions is sought, indicating some confusion about the correct approach. The conversation highlights the importance of understanding the relationship between angular velocity and the total number of revolutions over time. Accurate calculation methods are essential for solving angular motion problems effectively.