Another Newton's Law of Motion Problem.

[Elkay]

Due to a jaw injury, a patient must wear a strap (see the figure) that produces a net upward force of 5.00 N on his chin. The tension is the same throughout the strap. To what tension must the strap be adjusted to provide the necessary upward force? Here's the picture:

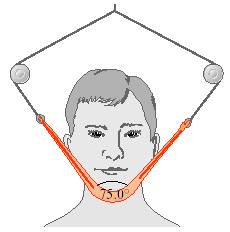
I think the tension for both sides of the strap will be equal, and the sum of all forces should equal zero. I'm also thinking that the sum of all forces should be zero if this is at equilibrium.
This is what I've done so far (hopefully my handwriting isn't too bad):
http://home.earthlink.net/~copper017/Random/freebody.jpg
http://home.earthlink.net/~copper017/Random/equations.jpg


I'm under the impression that this problem should be simple, but I've been looking at it and trying to do different things to it yesterday.

 

[cristo]

That's correct; you can now use the second equation to obtain the tension in the strap (since T1=T2).

 

[Hootenanny]

Your on the right lines; however, there is no need to consider the weight of the head in this case, we don't actually know the weight of the head, you've just assumed it be the same as the required net upwards force. The important point to remember is the required upward force is provided by the sum of the vertical components of both tensions. Neverless, either way you consider the problem you will obtain the same equations, as you have done correctly above. As you correctly said above, due to the symmetry of the problem, both tensions we be equal (i.e. T₁=T₂=T). Using this, can you simplify your expression for \sum F_y?

Edit: That's twice cristo ...

 

[Elkay]

Hmm, if I don't consider the weight, just look at the \sum F_y equation and solve for T1, the answer I got was -5...




http://home.earthlink.net/~copper017/Random/revise.jpg

 

[Hootenanny]

It is true that you don't need to consider weight here. However, you should consider the required upward force. RE:

The important point to remember is the required upward force is provided by the sum of the vertical components of both tensions.

Hence, you should obtain;

\sum F_y = T_1\sin52.5 + T_2\sin52.5 = 5

Which, by coincidence is identical to your second equation above.

 

[Elkay]

Thank you so much. I think I got the right answer:

http://home.earthlink.net/~copper017/Random/final1.jpg

Since T1=T2=T, then:
http://home.earthlink.net/~copper017/Random/final2.jpg So I guess the key to solving a problem like this is to recognize that the forces are in equilibrium, and to simplify the equations before attempting to solve. Hopefully my text will have a similar problem so I can practice some more.