- 1,277
- 1,078
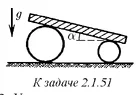
A slab rests on two massless rollers of different radii such that the angle of the slab's inclination is ##\alpha##. There is no slipping between the slab and the rollers, nor between the rollers and the ground. Prove that the slab moves with purely translational motion and find its acceleration.
(the value of the acceleration is ##g\sin(\alpha/2)##)
The standard obstacle here is finding the reactions of the rollers, but the use of the energy integral allows one to avoid this difficulty. Accurate proof that the motion is translational also requires some kinematic techniques.
It is also interesting to note that the hypothesis of ideal constraints here does not imply that the reactions of the rollers are perpendicular to the slab. This is not the case, even though the rollers are massless. It is because the net reaction is perpendicular to the virtual displacement, as it must be
(the value of the acceleration is ##g\sin(\alpha/2)##)
The standard obstacle here is finding the reactions of the rollers, but the use of the energy integral allows one to avoid this difficulty. Accurate proof that the motion is translational also requires some kinematic techniques.
It is also interesting to note that the hypothesis of ideal constraints here does not imply that the reactions of the rollers are perpendicular to the slab. This is not the case, even though the rollers are massless. It is because the net reaction is perpendicular to the virtual displacement, as it must be
Attachments
Last edited: