SUMMARY
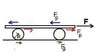
The discussion revolves around solving a physics problem involving rotational dynamics, specifically concerning a plank and two cylindrical rollers. The key parameters include a plank mass of 5.60 kg, roller radius of 4.40 cm, and a pulling force of 6.40 N. Participants provided insights on deriving the initial acceleration of the plank and the rollers, emphasizing the importance of free body diagrams and torque equations. The conversation highlighted the need to account for frictional forces and the relationship between linear and angular acceleration to arrive at accurate solutions.
PREREQUISITES
- Understanding of Newton's second law (F = ma)
- Familiarity with rotational dynamics and torque (Ʃτ = Iα)
- Knowledge of free body diagrams for analyzing forces
- Concept of rolling without slipping and its implications
NEXT STEPS
- Study the relationship between linear and angular acceleration in rotational systems
- Learn about the parallel axis theorem and its application in calculating moment of inertia
- Explore the concept of friction in rotational motion, particularly rolling friction
- Practice solving similar problems involving multiple bodies and forces in rotational dynamics
USEFUL FOR
Students taking introductory physics courses, particularly those focusing on mechanics and rotational dynamics, as well as educators seeking to enhance their teaching methods in these topics.