Another Two-dimensional Dynamics Problem

[mst3kjunkie]

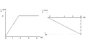
18. A particle starts from rest at r0=9.0 j(unit vector) m and moves in the xy-plane with the velocity shown in the figure below. the particle passes through a wire hoop located at r1=20i m, then continues onward.

a. At what time does the particle pass through the hoop?
b. What is the value of v4y, the y-component of the particle's velocity at t=4s?

c. Calculate and plot the particle's trajectory from t=0 to t=4s

I know how to do part c, but can't do it without parts a and b. So far all I've done is sketch out the graphs on my paper as well as the graphs of their derivatives. Thefigure referenced in the problem is the following:

https://www.physicsforums.com/attachment.php?attachmentid=7841&stc=1&d=1159234661
graphs.JPG

 

[mst3kjunkie]

solved problem.

 

[Astronuc]

Divide the problem into two parts:

Part 1, the particle undergoes constant acceleration in the x direction, up to 2 seconds (based on the graph), so determine how far the particle goes in the x-direction in two seconds.

Part 2, the particle travels at constant x-velocity passing through the hoop.

Now, if the particle travels along the line from the beginning (0,9) to the hoop (20, 0), their is a definite relationship between y and x, and therefore between v_y = dy/dt and v_x = dx/dt.

find y = mx + b, then dy/dt = m dx/dt.

 

[macgirl06]

help

I still don't understand, what would I do with y=mx+b once I find it, how can I find time?

 

[Astronuc]

Welcome back to PF, macgirl06.

I was wondering, is the graph on the right supposed to be a plot v_y(t) rather than v_x(t),

The two graphs result in a parametric problem.

v_x(t) and v_y(t) are independent of each other, but they depend on time, the independent variable. There is however a relationship between the velocities by virtue of common dependence on t.

Now v_x(t) is constantly increasing from t=0 to t=2 (approximately), and then is constant thereafter.

v_x(t) = 5t, so that at t=0, v_x(0) =0, and
v_x(2) = 10, and thereafter stays constant.

v_y(0) = 0 and v_y(4) = v_4y ??

Then one can integrate v(t) with respect to t,

x(t)\,=\,\int_{t_0}^t\,v(t)\,dt\,=\,x(t)\,-\,x_0 and similarly for y(t).

See - http://hyperphysics.phy-astr.gsu.edu/hbase/acons.html#c3 and the other plates on that page.

In the case of taking x(t) and y(t) and finding a formula as y = mx + b, time is simply removed. However, in the problem given, one still needs two equations because the behavior of x(t) is different in the two intervals.

One can also take x(t) and find t(x) to solve for t.