- #1
SilverSoldier
- 26
- 3
- Homework Statement
- I'm interested in finding a mathematical model that can be used to determine the positions of each point on a circular body having radius ##r##, rotating initially at an angular velocity ##\omega_0##, placed on a surface with friction. Suppose the friction causes a linear deceleration of ##a##, and angular deceleration of ##\alpha##.
- Relevant Equations
- Equations of linear and angular motion with constant acceleration
Basically, I want to know if my assumptions and workings are correct.
This is how I see this situation.
First, I'm viewing this body as a series of disconnected points, like I have in this animation I made, modeling purely rolling motion. Modeling the body like that worked in that case, and I'm assuming it will work here too. Please tell me if I am wrong.
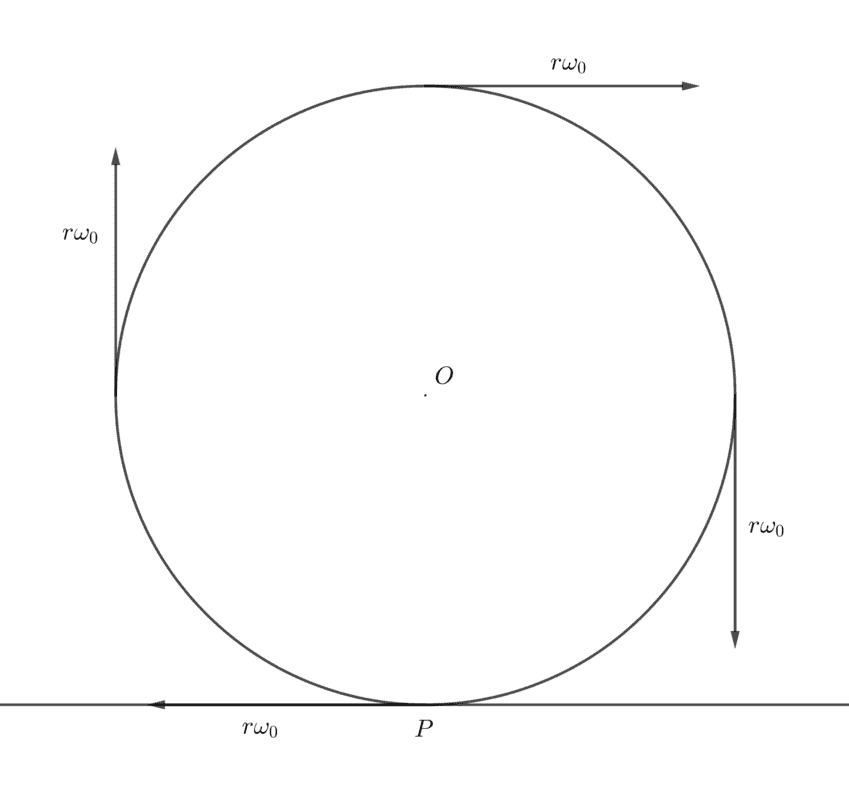
Suppose ##P## to be the point that first contacts the surface. Because this body was initially rotating, this point would want to move backward relative to the surface, with velocity ##r\omega_0##.
So kinetic friction will act, and the object will be accelerated forward. First, does kinetic friction act only on this contact point? Or else, does it act on all points, and accelerate all points on the object at the same rate?
If the latter is true (and I have assumed it is true in my model), then it must further increase the velocity ##r\omega_0## of the topmost point making it move rapidly forward, and increase the horizontal velocity components of the other points above the midpoint, causing them also to move forward, whereas the lower points will be made to move backward. How is this possible?
Clearly, all points must move backward, until the object gets into purely rolling motion.
This is how I have actually modeled the object using the above assumptions.
First, because all points accelerate forward at ##a##, at a given time ##t##, their horizontal translational velocity component would be given by ##at##. The object's angular velocity ##\omega## at the same time will be given by ##\omega_0-\alpha t##, so the tangential velocity of a point due to its rotation would be ##r(\omega_0-\alpha t)##.
Thus, the net horizontal velocity of the contact point at time ##t## would be ##at-r\omega_0+r\alpha t##. When this horizontal velocity becomes ##0##, friction will stop acting, and the object will start purely rolling. That is, at time ##t=\dfrac{r\omega_0}{a+r\alpha}##, it would start purely rolling.
Consider a general position ##P'## of point ##P##. Suppose it would have turned through an angle ##\theta## with respect to the new contact point. Let the translational velocity acting on it be ##v_t##, and its tangential velocity due to rotation be ##v_r##.
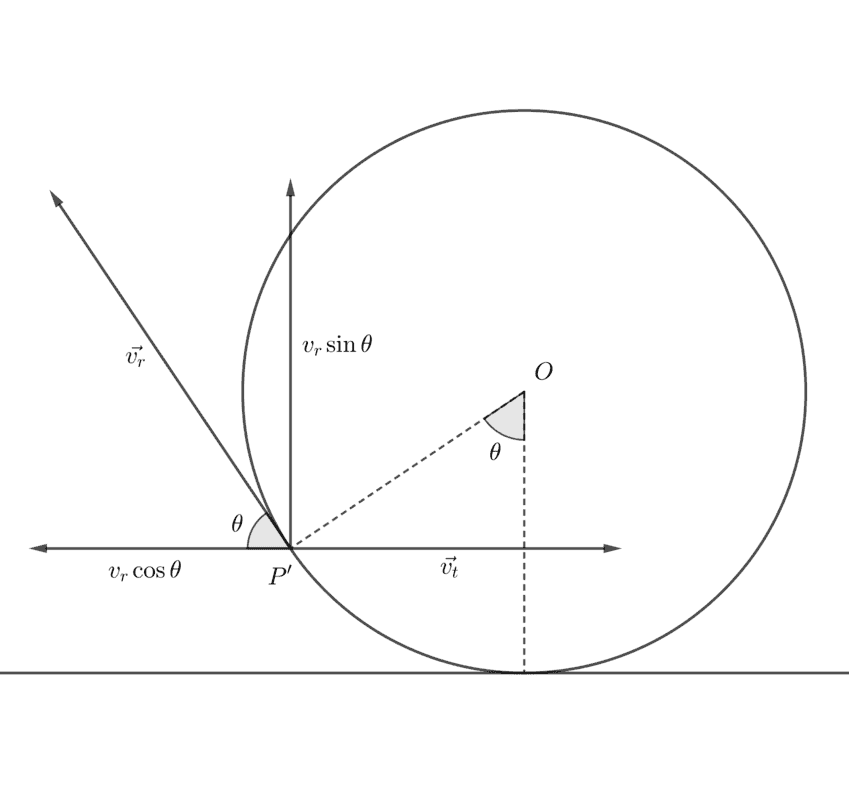
I can come up with the following definitions for ##\theta##, ##v_r## and ##v_t## as functions of time ##t##, as follows. Do point out any errors in them, if there are any.
$$
\theta(t)=\begin{cases}
\omega_0t-\dfrac{1}{2}\alpha t^2, & t\le \dfrac{r\omega_0}{a+r\alpha}\\
\\
\dfrac{r\omega_0^2}{a+r\alpha}-\dfrac{\alpha}{2}\left(\dfrac{r\omega_0}{a+r\alpha}\right)^2+\left(\omega_0-\dfrac{\alpha r\omega_0}{a+r\alpha}\right)\left(t-\dfrac{r\omega_0}{a+r\alpha}\right), & t >\dfrac{r\omega_0}{a+r\alpha}\\
\end{cases}
$$
$$
v_r(t)=
\begin{cases}
r(\omega_0-\alpha t), & t\le \dfrac{r\omega_0}{a+r\alpha}\\
\\
r\left(\omega_0-\dfrac{\alpha r\omega_0}{a+r\alpha}\right), & t > \dfrac{r\omega_0}{a+r\alpha}\\
\end{cases}
$$
$$
v_t(t)=
\begin{cases}
at, & t\le \dfrac{r\omega_0}{a+r\alpha}\\
\\
\dfrac{a r\omega_0}{a+r\alpha}, & t > \dfrac{r\omega_0}{a+r\alpha}\\
\end{cases}
$$
Therefore, supposing the coordinates of ##P## on an ##xy## plane are ##(0,0)##, I can obtain the ##x## and ##y## coordinates ##(x(T), y(T))## of ##P## at any time ##T## where
$$
x(T)=\int_0^T v_t(t)-v_r(t)\cos\theta(t)dt,
$$
and
$$
y(T)=\int_0^T v_r(t)\sin\theta(t)dt.
$$
That's about it.
My question is if this approach is correct, or if there's anything wrong in it. By the way, I have very little knowledge of integration; I just know that the area under a velocity vs. time graph gives displacement , and I would appreciate it if you could explain everything in the simplest terms possible.
, and I would appreciate it if you could explain everything in the simplest terms possible.
Thank you very much for taking your time

This is how I see this situation.
First, I'm viewing this body as a series of disconnected points, like I have in this animation I made, modeling purely rolling motion. Modeling the body like that worked in that case, and I'm assuming it will work here too. Please tell me if I am wrong.
Suppose ##P## to be the point that first contacts the surface. Because this body was initially rotating, this point would want to move backward relative to the surface, with velocity ##r\omega_0##.
So kinetic friction will act, and the object will be accelerated forward. First, does kinetic friction act only on this contact point? Or else, does it act on all points, and accelerate all points on the object at the same rate?
If the latter is true (and I have assumed it is true in my model), then it must further increase the velocity ##r\omega_0## of the topmost point making it move rapidly forward, and increase the horizontal velocity components of the other points above the midpoint, causing them also to move forward, whereas the lower points will be made to move backward. How is this possible?
Clearly, all points must move backward, until the object gets into purely rolling motion.
This is how I have actually modeled the object using the above assumptions.
First, because all points accelerate forward at ##a##, at a given time ##t##, their horizontal translational velocity component would be given by ##at##. The object's angular velocity ##\omega## at the same time will be given by ##\omega_0-\alpha t##, so the tangential velocity of a point due to its rotation would be ##r(\omega_0-\alpha t)##.
Thus, the net horizontal velocity of the contact point at time ##t## would be ##at-r\omega_0+r\alpha t##. When this horizontal velocity becomes ##0##, friction will stop acting, and the object will start purely rolling. That is, at time ##t=\dfrac{r\omega_0}{a+r\alpha}##, it would start purely rolling.
Consider a general position ##P'## of point ##P##. Suppose it would have turned through an angle ##\theta## with respect to the new contact point. Let the translational velocity acting on it be ##v_t##, and its tangential velocity due to rotation be ##v_r##.
I can come up with the following definitions for ##\theta##, ##v_r## and ##v_t## as functions of time ##t##, as follows. Do point out any errors in them, if there are any.
$$
\theta(t)=\begin{cases}
\omega_0t-\dfrac{1}{2}\alpha t^2, & t\le \dfrac{r\omega_0}{a+r\alpha}\\
\\
\dfrac{r\omega_0^2}{a+r\alpha}-\dfrac{\alpha}{2}\left(\dfrac{r\omega_0}{a+r\alpha}\right)^2+\left(\omega_0-\dfrac{\alpha r\omega_0}{a+r\alpha}\right)\left(t-\dfrac{r\omega_0}{a+r\alpha}\right), & t >\dfrac{r\omega_0}{a+r\alpha}\\
\end{cases}
$$
$$
v_r(t)=
\begin{cases}
r(\omega_0-\alpha t), & t\le \dfrac{r\omega_0}{a+r\alpha}\\
\\
r\left(\omega_0-\dfrac{\alpha r\omega_0}{a+r\alpha}\right), & t > \dfrac{r\omega_0}{a+r\alpha}\\
\end{cases}
$$
$$
v_t(t)=
\begin{cases}
at, & t\le \dfrac{r\omega_0}{a+r\alpha}\\
\\
\dfrac{a r\omega_0}{a+r\alpha}, & t > \dfrac{r\omega_0}{a+r\alpha}\\
\end{cases}
$$
Therefore, supposing the coordinates of ##P## on an ##xy## plane are ##(0,0)##, I can obtain the ##x## and ##y## coordinates ##(x(T), y(T))## of ##P## at any time ##T## where
$$
x(T)=\int_0^T v_t(t)-v_r(t)\cos\theta(t)dt,
$$
and
$$
y(T)=\int_0^T v_r(t)\sin\theta(t)dt.
$$
That's about it.
My question is if this approach is correct, or if there's anything wrong in it. By the way, I have very little knowledge of integration; I just know that the area under a velocity vs. time graph gives displacement
Thank you very much for taking your time