Niaboc67
- 249
- 3
Thanks
The discussion centers on the mathematical expression ##\log(x^2-25)## and its validity under certain conditions. Participants clarify that the expression is defined for all ##x## such that ##|x|>5##, while ##\log(x-5)## is only valid for ##x>5##. This distinction is crucial as it explains why the expression cannot be rewritten as ##\log(x+5)+\log(x-5)## without losing its original domain. The incorrect marking of the answer may stem from an automated system misinterpreting the notation used.
PREREQUISITESMathematics students, educators, and anyone involved in teaching or learning logarithmic functions and polynomial expressions.
It is correct, but you can expand x2-25 further. And note that |x|>5Niaboc67 said: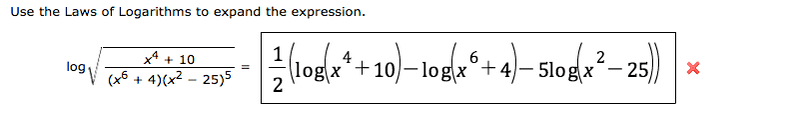
Thanks
What ehild means in the last sentence is that you must have |x| > 5.ehild said:It is correct, but you can expand x2-25 further. And note that |x|>5
No, what he's saying is that you can factor x2 - 25.Niaboc67 said:so instead of 25 it would be 5?
Yes, the expression can not be really expanded further for all x. Why was it marked incorrect then?Fredrik said:The original expression is defined for all ##x## such that ##|x|>5##. (These values of ##x## make the thing under the square root positive). But ##\log(x-5)## is defined for all ##x## such that ##x>5##. So ##\log(x-5)## isn't defined for all ##x## such that the original expression makes sense. This seems like a good reason to not do the rewrite ##\log(x^2-25)=\log(x+5)+\log(x-5)##.
Just to be clear, that should be x2 - 25.Niaboc67 said:I understand now. The x-25 could have been factored more. Thanks guys!
The ##x^2-25## can be factored, but we also said that it shouldn't be, because you don't want a final answer that makes sense for a smaller set of values of ##x## than the original expression. For example, the original expression makes sense when ##x=-7##, but an expression that contains ##\log(x-5)## doesn't. So we don't know why the answer you posted was marked incorrect. See BruceW's post for a possible reason.Niaboc67 said:I understand now. The x-25 could have been factored more. Thanks guys!