Application point of the lift force and pitching moment

[fog37]

Hello

As the angle of attack of an airfoil changes, the lift force $L$ changes both in magnitude and position (not in direction, always upward). The force location is a point called the center of pressure $x_{cp}$. It is possible to transfer the force to any another different point along the chord (even if it is always physically applied to $x_{cp}$). But that transfer implies that we add a pure couple moment $M$. However, as we change the AoA, the pure couple moment $M$ varies, i.e. it is dependent on the AoA even if we keep the reference point about which we calculate the moment fixed.

However, there is a special point called the aerodynamic center $x_{ac}$, located at a quarter chord distance from the leading edge $LE$. If the lift force $L$ is transferred to $x_{ac}$ as its application point, this pure couple moment $M_{ac}$ does NOT vary with AoA. Is that correct? This pure couple moment is always nonzero, even when $L=0$, for any AoA, and always equal to zero for a symmetric airfoil.

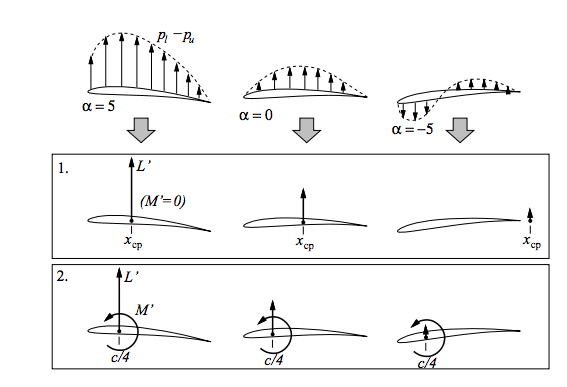
I believe, not sure if correct though, that if we leave the lift force $L$ at the center of pressure $x_{cp}$ and calculate the moment of the lift force $L$ about the aerodynamic center, with the lever arm being the distance $|x_{cp} - x_{ac}|$, the resulting moment
$|M|$ = $L |x_{cp} - x_{ac}|$ remains constant and is independent of the angle of attack even if both the distance $|x_{cp} - x_{ac}|$ and $|L|$ change with AoA . Is that correct? Also, this moment happens to be equal to the constant pure couple moment $M=M_{ac}$ described in the first paragraph...

Thanks and any clarification and validation!

 

[fog37]

Hopefully, just to add clarity to my question, here another picture illustrating the lift force $L$ applied at the center of pressure $CP$, which varies with AoA. If the pitching moment due to $L$ is calculated about the aerodynamic center $AC$, the moment remains constant: even if the magnitude of $L$ increases from $L_1$ to $L_2$, the lever arm $d$ decreases from $d_1$ to $d_2$ keeping the moment constant...

The second figure shows how the force can be moved to different points of applications causing the moment $M$ to change depending on the application point. But only when the force is applied at c/4 the moment remains constant with AoA.

 

[CWatters]

However, there is a special point called the aerodynamic center xacxacx_{ac}, located at a quarter chord distance from the leading edge LELELE. If the lift force LLL is transferred to xacxacx_{ac} as its application point, this pure couple moment MacMacM_{ac} does NOT vary with AoA. Is that correct?

Yes. In fact the definition of the aerodynamic centre is the point at which the pitching moment does not change significantly with angle of attack.

See also..

https://en.wikipedia.org/wiki/Pitching_moment

This pure couple moment is always nonzero, even when L=0L=0L=0, for any AoA, and always equal to zero for a symmetric airfoil.

Typically it's negative (nose down) for "normal" cambered wings. Zero for symmetrical wings and can be positive for wing sections used on tailless aircraft.

There is an interesting intro to stability here..

http://www.mh-aerotools.de/airfoils/flywing1.htm
See the table below "Equilibrium". It explains why conventional wing sections need a tail and how sections with a positive pitching moment are used on tailless aircraft. Its been awhile since I looked at this stuff so might not be able to answer all questions.

 

[fog37]

Thank you CWatters!

I found figure that may be useful for other readers like me. For the same aerofoil, the figure shows how the pitching moment $C_m$ is constant if the moment is calculated choosing AC as the reference point (lever arm is distance from $AC$ to the lift force $L$). In other cases, the coefficient varies linearly with AoA:

"...Yes. In fact the definition of the aerodynamic centre is the point at which the pitching moment does not change significantly with angle of attack..."

I still think it is so cool that there is such a point AC such that the pitching moment due to the lift force F remains constant as the AoA changes. This constancy derives from the fact that the lift force magnitude, the lift force location and lift force distance from AC all change with changing AoA but the product $M=L d$ stay constant.

I guess there is a similar point for the rolling moment such that the rolling moment stays constant as the AoA changes?

 

[FactChecker]

It has never been clear to me why using the AC would simplify calculations. Doesn't the AC move when the flight condition changes and how can its position be determined? How hard can it be to add a linear function of AOA? Many people who use the data use a reference position for moments that is not at the AC. I think that the wind tunnel measurements are not done at the AC.

 

[fog37]

My understanding is that the AC is a fixed point about 0.25 chord distance from the leading edge of the airfoil and stays there. Mathematically, the moment due to lift force calculated about AC is constant (approximately) with varying AoA.

Like you, I am not sure about the real value of using the AC but those who make serious aerodynamic calculations seem to think it is very convenient...

 

[CWatters]

Like I said before. The definition of the AC is the point at which the pitching moment is (reasonably) constant with angle of attack.

Consider an all moving rudder on an aircraft or boat (eg no fixed fin). If its not balanced eg its just a plate hinged at the front edge, then there is a massive pitching moment that tends to keep it centred and requires large forces to overcome. The pitching moment varies with angle of attack and changes sign at the centre.

As you move the hinge point back, so that some area is in front of the hinge, it becomes more and more aerodynamically balanced until there is a point where the pitching moment approaches zero and independent of the angle of attack. That's the AC.

 

[anorlunda]

As you move the hinge point back, so that some area is in front of the hinge, it becomes more and more aerodynamically balanced until there is a point where the pitching moment approaches zero and independent of the angle of attack.

Yes indeed. In boating, we call that a balanced rudder.