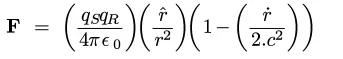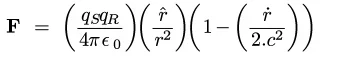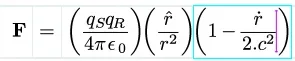stovenn
- 3
- 2
- TL;DR Summary
- I am using Gauss's 1835 formula to try and derive the expression for the perpendicular force between two infinitely-long, parallel wires carrying steady DC currents. I obtain a formula that looks the correct shape and pattern but gives the wrong direction and magnitude for the force.
Please can anyone either:-
(1) point me to a derivation of the perpendicular force (Fy) between two very long parallel wires carrying steady currents utilising the formula of Gauss for the force F along the line r between 2 charges?
Or alternatively (2) point out where I have gone wrong in my method?
I am having problems with calculating the direction and magnitude of the force as expected from modern (Biot-Savart-Maxwell-Lorentz) formula.
Here is my method and results so far:-

This wikipedia page (https://en.wikipedia.org/wiki/Weber_electrodynamics) indicates that Gauss's formula is the same as Weber's but without the final acceleration terms:-
F=(qs.qr/4.pi.e0.r^2).( 1 - (1/2.c^2)*(dr/dt)^2 )...where dr/dt is the radial velocity.
I am using dr/dt=(Vr-Vs)*cosTheta where Vs, Vr are the velocities (in the x-direction) of the source and receiving charges. Theta is the angle between the x-axis and line r connecting the 2 charges and for a given source position P at distance X along the x-axis from the receiver theta is given by cosTheta=(-X/r).
I obtain an expression for Fy for a source charge at [X,0] and a receiver charge at [0,h]...
=(qs.qr/4.pi.e0.r^2).(h/r).( 1 - (1/2.c^2)*(dr/dt)^2 )
= (qs.qr/4.pi.e0.r^2).(h/r).( 1 - (1/2.c^2)*(Vs^2 + Vr^2 -2.Vr.Vs)*(X^2/r^2) )
Then I calculate the net Fy force over the 4 interactions between two "current elements" (source proton or source drift electron) and (receiver proton or receiver drift electron):-
Fy= (qs.qr/4.pi.e0).(hX^2/r^5).( Vr.Vs/c^2)
Integrating (hX^2/r^5) over -infinity<x<+infinity -->(2/3h)
So the total force exerted by the source wire upon the receiver current element (divided by the number of source current elements per unit length of wire):-
FY= (qs.qr/4.pi.e0).(2/3h).( Vr.Vs/c^2)
= (qs.qr/2.pi.h.e0).(1/3).( Vr.Vs/c^2).
And if the number of source current elements per unit length of wire is the same in both wires then FY also indicates the force received per unit length of the receiver wire.
= = = = = = =
Compared to the result from textbook formulae this value of FY is in the opposite direction and only (1/3) of the correct magnitude.
(1) point me to a derivation of the perpendicular force (Fy) between two very long parallel wires carrying steady currents utilising the formula of Gauss for the force F along the line r between 2 charges?
Or alternatively (2) point out where I have gone wrong in my method?
I am having problems with calculating the direction and magnitude of the force as expected from modern (Biot-Savart-Maxwell-Lorentz) formula.
Here is my method and results so far:-
This wikipedia page (https://en.wikipedia.org/wiki/Weber_electrodynamics) indicates that Gauss's formula is the same as Weber's but without the final acceleration terms:-
F=(qs.qr/4.pi.e0.r^2).( 1 - (1/2.c^2)*(dr/dt)^2 )...where dr/dt is the radial velocity.
I am using dr/dt=(Vr-Vs)*cosTheta where Vs, Vr are the velocities (in the x-direction) of the source and receiving charges. Theta is the angle between the x-axis and line r connecting the 2 charges and for a given source position P at distance X along the x-axis from the receiver theta is given by cosTheta=(-X/r).
I obtain an expression for Fy for a source charge at [X,0] and a receiver charge at [0,h]...
=(qs.qr/4.pi.e0.r^2).(h/r).( 1 - (1/2.c^2)*(dr/dt)^2 )
= (qs.qr/4.pi.e0.r^2).(h/r).( 1 - (1/2.c^2)*(Vs^2 + Vr^2 -2.Vr.Vs)*(X^2/r^2) )
Then I calculate the net Fy force over the 4 interactions between two "current elements" (source proton or source drift electron) and (receiver proton or receiver drift electron):-
Fy= (qs.qr/4.pi.e0).(hX^2/r^5).( Vr.Vs/c^2)
Integrating (hX^2/r^5) over -infinity<x<+infinity -->(2/3h)
So the total force exerted by the source wire upon the receiver current element (divided by the number of source current elements per unit length of wire):-
FY= (qs.qr/4.pi.e0).(2/3h).( Vr.Vs/c^2)
= (qs.qr/2.pi.h.e0).(1/3).( Vr.Vs/c^2).
And if the number of source current elements per unit length of wire is the same in both wires then FY also indicates the force received per unit length of the receiver wire.
= = = = = = =
Compared to the result from textbook formulae this value of FY is in the opposite direction and only (1/3) of the correct magnitude.
Last edited: